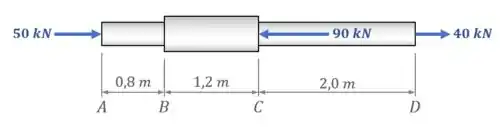
O eixo de aço abaixo possui, nos trechos e , uma seção transversal com uma área de , e, no trecho , uma seção transversal com uma área de .
Determine a variação de comprimento total do eixo quando ele está submetido às cargas mostradas na figura, sabendo que ele possui um módulo de elasticidade .
Passo 1
Nesse exercício, queremos encontrar a variação de comprimento do eixo quando ele está submetido ao carregamento mostrado.
Agora, lembra aí!
Já existe uma fórmula para encontrar a variação de comprimento em uma peça com base nas forças que atuam nela:
Nessa fórmula, é a força interna normal, é o comprimento original, é o módulo de elasticidade e é a área da seção transversal da peça. Repare que o enunciado forneceu todos esses valores!
Mas no nosso caso, o eixo tem diferentes trechos (, e ) com diferentes valores de , e .
Então a variação de comprimento total do nosso eixo vai ser a soma das variações de comprimento de cada trecho:
Passo 2
Aplicando a fórmula para cada trecho, e sabendo que o módulo de elasticidade é o mesmo para toda a peça, temos que:
Então para resolver o nosso exercício, precisamos identificar os valores de , e para cada trecho, e, em seguida, aplicar a fórmula acima.
Do enunciado, temos que:
.
E da figura, temos que
Só falta identificar então as forças normais , que precisam ser encontradas através de uma análise de esforços internos nas diferentes seções do eixo.
Mas atenção! A variação do comprimento de cada trecho pode ser positiva OU negativa. O que vai determinar isso é o sinal de .
Isso significa que vamos ter que respeitar as convenções de sinais das forças internas na hora de calcular os valores de , e !
Passo 3
Vamos começar então fazendo uma análise de esforços internos para encontrar os valores das forças internas normais nas diferentes seções do eixo.
1. Começando pelo trecho AB, essa análise fica assim:
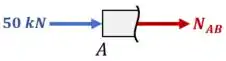
Aplicando o equilíbrio de forças na horizontal, temos:
O que significa que:
2. Já para as seções entre B e C, temos:
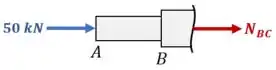
Aplicando o equilíbrio de forças:
De tal forma que:
3. E, finalmente, para o trecho CD:

Aplicando o equilíbrio de forças:
O que significa que:
Passo 4
Encontrados os valores das forças normais , podemos aplicar a fórmula:
Substituindo todos os valores, temos:
Pausa para prestar atenção nas unidades!
Podemos substituir por . Dessa forma, as unidades e vão se cortar e só vai sobrar para o resultado a unidade (metros).
Calculando cada variação individualmente, isso fica assim:
Dá para ter uma noção melhor de cada deformação se reescrevermos elas em :
Somando as deformações individuais de cada trecho, encontramos a deformação total :