Exercícios Resolvidos de Deformação e a Lei de Hooke

Exercício 8 1 2 3 4 5 6 7 9 10 11 12

Enunciado

A barra rígida é sustentada por um pino em e pelos cabos e . Se a carga aplicada à viga provocar um deslocamento de para baixo na extremidade , determine a deformação normal desenvolvida nos cabos e .

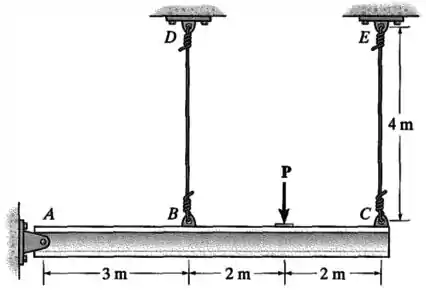
Passo 1

Ambos os cabos tem comprimentos iniciais iguais .

O cabo sofre uma variação de comprimento .

Consequentemente o cabo vai sofrer uma variação de comprimento proporcional a , de acordo com a semelhança de triângulos abaixo:

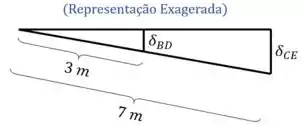
Dessa semelhança de triângulos, tiramos que está para assim como está para , de tal forma que:

Agora que temos em mãos os comprimentos iniciais e as deformações para os cabos e , podemos calcular as deformações nesses cabos:

Substituindo e substituindo os valores de , e , temos:

Agora, temos que tomar um pouco de cuidado uma vez que as deformações devem ser adimensionais.

Isso significa que as unidades em cima e em baixo dessas equações precisam ser iguais.

Podemos ajeitar isso reescrevendo o comprimento de como :

Calculando tudo, isso dá:

Resposta

Exercícios de Livros Relacionados

Para o reservatório de ar comprimido do P r o b . 6.104 , determinar a maior pressão admissível, sabendo-se que a tensão normal admissível perpendicular a solda é de 165M p a e a tensão admissível de

As deformações específicas normais determinadas com o uso da roseta da figura, colada na superfície de um componente estrutural, são: ε 1 = - 93,1μ ε 2 = - 385μ ε 3 = + 210μ Determinar: (a) a orientaç

Para o dado estado plano de deformação, usar o método da S e c .6.10 para determinar o estado de deformação associado aos eixos x ’ e y ’ , que foram girados de um ângulo θ , no sentido mostrado. ε x

Resolver o P r o b . 6.111 , assumindo que a força P é horizontal ( α = 0 ) Ponto L;

Um vaso de pressão de 300mm de diâmetro externo é fabricado com chapa de aço de 6,35mm de espessura, que é soldada ao longo de uma hélice formando um ângulo de 22,5 ° com a horizontal. Sabendo-se que