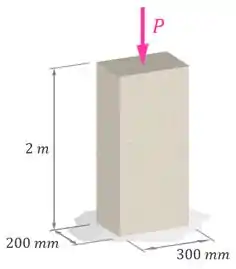
Uma coluna da figura é feita de um concreto com um módulo de elasticidade de . Determine a deformação , a variação de comprimento e o comprimento final dessa coluna quando ela estiver sob compressão por uma força de .
Passo 1
A força de compressão gera na coluna uma força interna normal , que, por sua vez, gera uma tensão normal média .
Para calcular essa tensão , podemos analisar os esforços internos na coluna para encontrar a força normal e usar as dimensões para encontrar a área da seção transversal.
Agora, de acordo com a Lei de Hooke, essa tensão vai corresponder a uma certa deformação na coluna:
Então conhecendo o módulo de elasticidade e a tensão , conseguimos encontrar a deformação na coluna, que é uma das coisas que o exercício quer que a gente determine.
Além disso, sabemos que a deformação é definida como:
E que a variação de comprimento é definida como:
Então sabendo que a coluna tinha um comprimento original , podemos usar as fórmula acima para encontrar a variação de comprimento e o comprimento final da coluna.
Passo 2
Vamos começar avaliando os esforços internos na coluna para encontrar o valor da força normal .
Desenhamos a coluna secionada, adicionamos a força externa e adicionamos a força interna normal apontando para fora da peça:
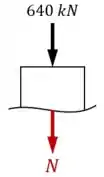
E em seguida, aplicamos o equilíbrio de forças na vertical para relacionar a força normal com a força externa:
Isolando , encontramos que:
Encontramos que a força normal é negativa, ou seja, ela é uma força normal de compressão.
Consequentemente, a tensão normal média e a deformação também vão ser negativas.
Passo 3
Com a força normal encontrada, já temos todas as informações necessárias para aplicar a Lei de Hooke:
Substituir a fórmula da tensão normal média :
E isolar a deformação :
Substituindo os valores , e , temos:
Como , as unidades dessa equação vão todas se cortar.
Calculando tudo, temos:
Essa já é uma das nossas respostas, agora vamos encontrar as outras duas!
Passo 4
Aplicando a fórmula da deformação :
Isolando a variação do comprimento :
Substituindo e , temos:
O que dá:
Como é o mesmo que , isso é o mesmo que:
Por última, a variação do comprimento é a diferença entre o comprimento final e o comprimento inicial :
Isolando o comprimento final , temos:
Substituindo e :
é o mesmo que ou , então:
Ou seja: