Os dois cabos estão interligados em . Se a força provocar um deslocamento horizontal de no ponto em , determine a deformação normal desenvolvida em cada cabo.
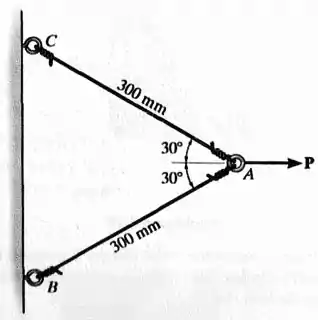
Passo 1
Os dois cabos tem comprimentos iniciais iguais .
Usando os ângulos fornecidos de , conseguimos deduzir:
- que a distância vertical entre os pontos e e entre os pontos e é igual à ;
- e que a distância entre o ponto e a parede é de ,
Como mostra a imagem abaixo:
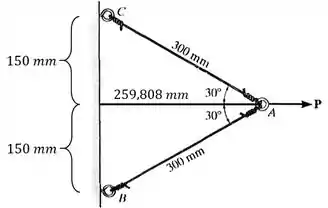
Quando o ponto se desloca para a direita, os cabos deixam de ter de comprimento e a distância entre a parede e o ponto sobe de para :
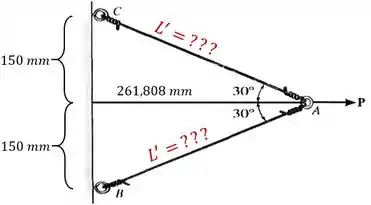
Para encontrar o comprimento final dos cabos, podemos usar o Teorema de Pitágoras:
Calculando, isso dá:
Agora que sabemos os comprimentos inicial e final , iguais para os dois cabos, podemos calcular a deformação nos cabos:
Substituindo os valores de e , temos:
Calculando tudo, isso dá: