O cabo de de diâmetro é feito de um aço com . Sabendo que a máxima tensão no cabo não pode exceder e que a deformação do cabo não deve exceder , determine a máxima força que pode ser aplicada conforme mostra a figura.
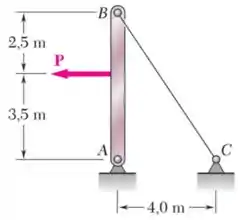
Passo 1
O que está acontecendo?
A viga é mantida em equilíbrio pelas reações horizontal e vertical do apoio em e por uma força “” feita pelo cabo , como mostra o seu DCL (diagrama de corpo livre):
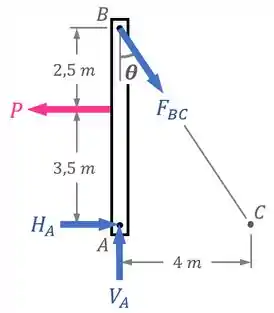
Como reação a essa força , a viga traciona o cabo com uma força de mesma intensidade .
Essa tração no cabo gera nele uma tensão normal média .
Quanto maior for a força , provavelmente maior será a força , de forma a garantir o equilíbrio da viga. Quanto maior for , maior será a tensão no cabo.
O cabo tem um diâmetro , é feito de um aço com módulo de elasticidade e possui um comprimento inicial que pode ser obtido através do teorema de Pitágoras:
E o que é que o exercício quer?
Ele quer saber o valor máximo da força tal que a tensão no cabo não ultrapasse e a variação de comprimento do cabo não ultrapasse :
Mas se a gente for parar pra pensar, essa variação de comprimento máxima corresponde a uma deformação máxima que corresponde a uma tensão máxima.
Então essas condições podem ser reescritas como:
Entre essas duas condições, a que resultar em valores mais restritos para vai ser a condição que vamos usar no restante do exercício, já que assim as duas condições vão estar sendo respeitadas.
Depois que tivermos definido a nossa condição limitante, vamos desenvolver nela a tensão normal média para encontrar o valor máximo da força .
Para tanto, vamos precisar ter antes aplicado as condições de equilíbrio no DCL da viga para encontrar a intensidade da tração no cabo em função da força .
Passo 2
Então primeiro, vamos descobrir qual é a nossa condição limitante:
ou...
Pegando a segunda condição e substituindo os valores:
- ;
- e ,
Temos:
Para comparar essa condição com a outra, vamos querer uma resposta em .
Então reescrevemos como e reescrevemos como :
Calculando tudo, isso dá:
Isso é menor que .
O que isso significa é que bem antes da tensão na corda atingir , a sua variação de comprimento já vai ter atingido (quando a tensão for de ).
Sendo assim, a nossa condição limitante para o restante do exercício vai ser:
Passo 3
Agora, antes de usar a condição para descobrir qual é o valor máximo de , precisamos descobrir como afeta a tensão normal média no cabo.
Como o cabo só está sobre tração por uma força de intensidade , então a força interna normal no cabo vai ser igual a .
Sendo assim, precisamos avaliar o equilíbrio da viga para encontrar em função da força .
Fazendo o Diagrama de Corpo Livre da viga, temos:
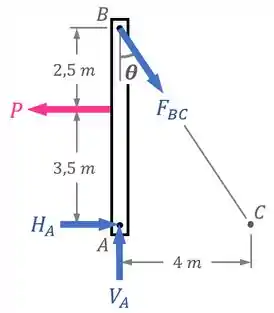
Agora vamos pensar...
Queremos relacionar e .
A condição de equilíbrio que vai nos permitir fazer isso mais facilmente vai ser aquela que não envolve as outras forças ( e ), que é o equilíbrio de momentos em relação ao ponto :
A força vai fazer um momento no sentido anti-horário () com um braço de .
Quanto a força ela vai ter:
- Uma componente vertical que não vai gerar momento (por ter um braço de );
- E uma componente horizontal que vai gerar um momento no sentido horário () com um braço de .
Então o somatório de momentos fica assim:
Isolando , temos:
Substituindo por :
Como a intensidade de é a mesma intensidade da tração no cabo e, consequentemente, a mesma intensidade da força normal no cabo, temos que:
Passo 4
Já sabemos como afeta a força normal e, consequentemente, a tensão no cabo.
Então já podemos aplicar a condição limitante:
Substituindo a fórmula da tensão normal média:
A área da seção transversal do cabo pode ser encontrada a partir de seu diâmetro de através da fórmula .
Substituindo isso e a expressão encontrada para no passo anterior, temos:
Isso é o mesmo que:
Simplificando e juntando tudo, isso fica assim:
Queremos descobrir o valor máximo de , então vamos isolá-lo:
Antes de calcular tudo, precisamos descobrir o valor de .
Observando a figura do exercício:
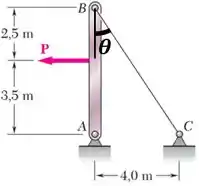
Vemos que o seno de é igual ao cateto de sobre a hipotenusa, que pode ser calculada pelo teorema de Pitágoras:
Substituindo esse seno e o diâmetro na equação anterior, temos:
Megapascal () é o mesmo que um newton por milímetro quadrado (), então o resultado desse cálculo vai sair em newtons ():
Esse número é um pouco grande, então podemos reescrevê-lo em :
O valor máximo de vai ocorrer quando essa expressão for uma igualdade, então: