Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação Diferencial da Onda

Ver Teoria
Exercício 912345678101112131415161718

Enunciado

Três ondas propagantes senoidais estão em cordas idênticas, com a mesma tensão. As formas matemáticas das ondas são:

y 1 x ,   t =   y m sin ⁡ 3 x   -   6 t ,  

y 2 x ,   t =   y m sin ⁡ 4 x   -   8 t e  

y 3 ( x ,   t ) = y m   s i n   ( 6 x   -   12 t )

onde x está em metros e t em segundos. Faça a correspondência de cada forma matemática ao gráfico apropriado abaixo.

  1. y 1 :   i ,   y 2 :   i i ,   y 3 :   i i i
  2. y 1 :   i i i ,   y 2 :   i i ,   y 3 :   i
  3. y 1 :   i ,   y 2 :   i i i ,   y 3 :   i i
  4. y 1 :   i i ,   y 2 :   i ,   y 3 :   i i i
  5. y 1 :   i i i ,   y 2 :   i ,   y 3 :   i i

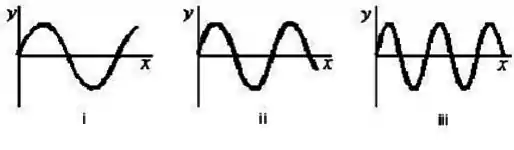
Passo 1

A equação de uma onda senoidal é:

y x ,   t =   y   m sin ⁡ k x   -   w t

Com k = 2 π λ   , e w = 2 π T .

Onde; k é o número de onda, λ é o comprimento de onda e w é a frequência angular.

Das equações descritas no enunciado, podemos obter nossos valores para a constante k :

k 1   = 3 ,

k 2   = 4   e

k 3   = 6

Passo 2

O comprimento de onda λ ,   é a menor distância entre dois pontos em concordância de fase.

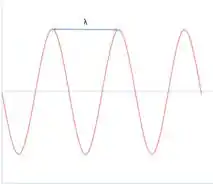
Dos gráficos dados no enunciado, vemos que a distância λ   i   >   λ   i i   >   λ   i i i .

Logo, como k = 2 π λ   , observamos que k é inversamente proporcional a λ ,

Portanto, analisando as equações nos leva a: k   i   <   k   i i   <   k   i i i

Resposta

Letra A

Exercícios de Livros Relacionados

Uma onda tem uma velocidade de 240 m s e um comprimento de onda de 3,2m . Qual é (a) a frequência e (b) o período da onda?
Uma onda possui uma frequência angular de 110r a d / s e um comprimento de onda de 1,80m . Calcule (a) o número de onda e (b) a velocidade da onda.
Três ondas, que têm a mesma frequência, o mesmo comprimento de onda e a mesma amplitude, viajam ao longo do eixo x . As três ondas são descritas pelas seguintes funções de onda: y 1 x , t = 5,00c ms e
A velocidade no vácuo das ondas eletromagnéticas (como as ondas de luz visível, as ondas de rádio e os raios X) é 3,0 × 10 8m / s . (a) Os comprimentos de onda da luz visível vão de aproximadamente 40
Uma onda humana. A ola é uma onda, criada pela torcida, que se propaga nos estádios em eventos esportivos (Figura). Quando a onda chega a um grupo de espectadores, eles ficam em pé com os braços levan