a) Mostre, por substituição direta, que (onde , são constantes) é solução da equação de onda se e determine a velocidade da onda em termos do comprimento de onda e do período .
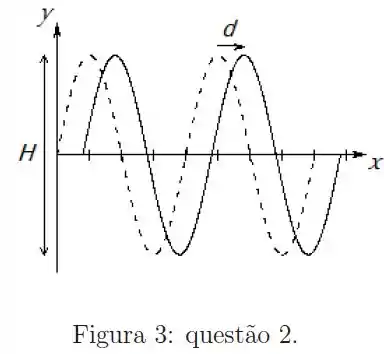
A figura 3 mostra o deslocamento tranversal ao longo de uma corda que suporta uma onda harmônica como a descrita no item anterior, em dois instantes de tempo, . Durante este intervalo de tempo, as cristas da onda deslocam-se de uma distância , como indica a figura. Nela, cada divisão do eixo horizontal vale e a distância entre as cristas e os vales é de .
b)Determine a amplitude da onda .
c)Determine o número de onda .
d)Determine a frequência angular .
e)Determine a constante de fase da onda.
Passo 1
a)
Vamos calcular cada uma das derivadas segunda e depois jogar na relação. Se encontrarmos uma igualdade verdadeira, teremos conseguido provar que é uma solução da equação de onda.
Jogando na equação:
Cortando dos dois lados:
Tirando a raiza quadrada nos dois lados:
Essa igualdade é verdadeira? Sim, uma velha conhecida nossa. Assim, concluímos, por substituição, que é uma solução da equação de onda.
Passo 2
b)
Pela figura, vemos que:
Passo 3
c)
Pra descobrir , basta a gente observar a figura pontilhada: Observe quantas divisões existem após passarem os dois picos que formam um ciclo completo da onda. Viu?
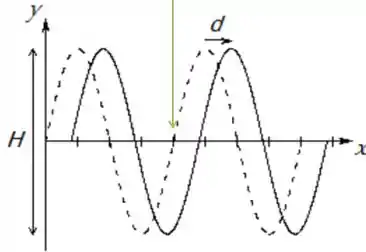
Assim, percebemos que:
Assim podemos determinar
Passo 4
d)
Peloe enunciado, sabemos que a onda se deslocou em um tempo
Assim:
Assim, usando:
Passo 5
e)
Podemos aplicar na equação de onda . Pelo gráfico, vemos que, nesse caso,
Assim:
y
Resposta
a)
Demonstração acima.
b)
c)
d)
e)