Na figura abaixo, a partícula se move ao longo da reta com uma velocidade constante paralela ao eixo . No instante de tempo em que a partícula passa pelo eixo , a partícula deixa a origem com velocidade inicial zero e aceleração constante de módulo , o ângulo entre e o semi-eixo positivo é .
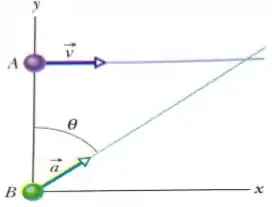
Escreva uma expressão para a velocidade da partícula .
Escreva uma expressão para a posição da partícula em função do tempo.
Escreva uma expressão para a posição da partícula em função do tempo.
Que valor de velocidade deve ter a particula para que aconteça a colisão?
Passo 1
Basta lembrar da fórmula que diz que . Mas como a velocidade inicial da partícula é nula e ela está inclinada aos eixos e , teremos que decompor ela assim:
Passo 2
Nessa teremos que lembrar da fórmula , a partícula não tem aceleração. Então vamos decompor nos eixos e assim:
Passo 3
Novamente vamos utilizar a fórmula , só que na partícula não tem velocidade inicial e a posição inicial é zero. Então vamos decompor assim:
Passo 4
Para que aconteça a colisão para o mesmo instante de tempo, assim obtemos:
Igualando em :
Igualando em :
E, portanto:
Resposta