O trem sai de uma estação a partir do repouso, rumo ao oeste, com aceleração constante de . Já o trem se move do norte para o sul com velocidade constante de , e passa por essa mesma estação segundos após a partida do trem . Considere o versos apontando para leste e o versor para o norte. Considere também a estação na origem do sistema de coordenadas, e considere o tempo inicial no instante em que o trem sai da estação.
Escreva uma equação cuja solução dê o instante de tempo em que a distância entre os trens é mínima (não precisa resolver). Essa distância mínima ocorre antes da passagem do trem pela estação? Justifique.
Passo 1
Eaew, tudo bem com você?
O enunciado nos descreve o movimento de dois trens, o trem que tem uma aceleração de , e a partir do repouso, se move para o oeste saindo de uma estação. O enunciado também indica a existência do trem que vem do norte para o sul à uma velocidade constante de , chegando a estação depois que o trem saiu! O esquema usando os versores indicados no enunciado é o seguinte
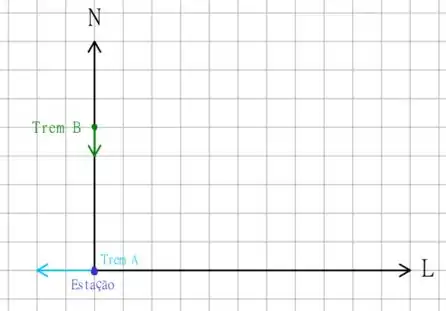
Na alternativa anterior nós obtivemos que o vetor posição relativa entre os dois trens é dada por
esta expressão será útil nesta alternativa pois a distância entre os dois trens é dada pelo módulo do vetor acima! A distância mínima é obtida analisando a primeira e segunda derivadas no tempo para obter um ponto crítico de mínimo, como em cálculo . Vamos fazer isso! Vem comigo!
Passo 2
Primeiro, vamos calcular o módulo do vetor distância relativa, temos que
Maravilha, e quais são os pontos críticos? Para isso, devemos ver quando a primeira derivada é zero, ou seja
Vamos precisar revisar como calcular essa derivada! Precisaremos usar a regra da cadeia e a regra do tombo! Vamos lá!
Passo 3
Primeiro, temos que a regra da cadeia é usada para funções compostas da forma
e, a derivada dessas funções é tal que
em nosso caso, temos que com . Pela regra do tombo, podemos escrever que
ou, reescrevendo a expressão acima, temos
De forma que a regra da cadeia resulta em
Precisamos agora resolver a derivada que falta! Vamos lá!
Passo 4
Primeiro, vamos lembrar que a derivada da soma é a soma das derivadas, portanto temos que
Pela regra do tombo podemos resolver a primeira derivada para obter que
para a segunda derivada, temos que usar a regra da cadeia novamente, mas agora, temos que e . De forma que
usando a regra do tombo, e também que
que resulta em
Juntando ambos os resultados, temos que a regra da cadeia é
e, portanto a derivada que precisamos resolver é
Vamos voltar para a expressão do ponto crítico! Vem comigo!
Passo 5
Temos usando a derivada que calculamos no último passo que
nos dá o ponto crítico da distância entre os dois trens! Podemos simplificar a expressão acima multiplicando ambos os lados por , de forma que obtemos o seguinte
ou se dividirmos ambos os lados por , temos que
Esta expressão nos dará o ponto crítico, podendo ser de máximo ou mínimo para a nossa distância! Para determinar se é um ponto crítico de mínimo, existe ainda mais uma condição que deve ser respeitada! Saca só!
Passo 6
Para que o ponto crítico encontrado seja um ponto de mínimo, é preciso que para o valor de no qual a primeira derivada é nula, também tenhamos que
usando o resultado que obtivemos no último passo, temos que
Aqui nós temos o quociente de duas funções da forma , a regra do quociente diz que
usando que e que , podemos escrever a seguinte relação
Vamos tentar simplificar esta expressão! Belezinha? Vem comigo!
Passo 7
Primeiro, como o denominador da desigualdade é sempre positivo, podemos simplesmente multiplicar tudo por , o que simplifica a nossa desigualdade, temos que
No passo anterior obtivemos que
quando avaliada nos pontos críticos, portanto, nos pontos que nos interessam, temos que
ou dividindo por , obtemos simplesmente que
Vamos calcular a derivada do lado esquerdo! Vamos precisar aplicar a regra do tombo somente! Vem comigo!
Passo 8
Expandindo nossa derivada, temos que
usando a regra do tombo, temos que
ou, simplesmente, temos que
Maravilha! Estas são as duas relações que estabelecem que o nosso tempo é um instante de distância mínima! A desigualdade acima juntamente com a necessidade de que
Como adendo da questão, SIM, isso ocorrerá antes de que o trem chegue até a estação. Note que, antes de chegar a estação, o trem tenta se aproximar do trem , enquanto o mesmo se afasta, no entanto, após chegar a estação, ambos os trens estão se afastando! A questão foi isso! Te vejo na próxima! Tchauzinho!
Resposta
A relação para o instante de tempo é com , e SIM, ocorrerá antes do trem chegar a estação!