Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Erros

Ver Teoria
Exercício 123456789101112131415

Enunciado

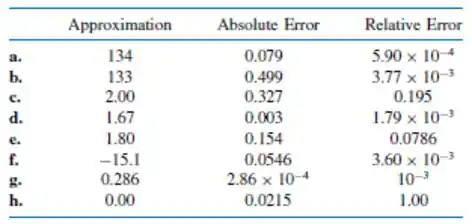
Usando um sistema de aritmética de ponto flutuante de 3 dígitos que utiliza arredondamento, faça os cálculos abaixo. Em seguida, calcule o erro absoluto e relativo de cada operação com pelo menos 5 dígitos.

a 133 + 0.921

b 133 - 0.499

c 121 - 0.327 - 119

d 121 - 119 - 0.327

e 13 14 - 6 7 2 e - 5.4

f - 10 π + 6 e - 3 62

g 2 9 ∙ 9 7

h π - 22 7 1 17

Passo 1

a

133 + 0.921 =

= 0.133 × 10 3 + 0.921 × 10 0 =

= 0.133 × 10 3 + 0.000921 × 10 3 =

= 0.133921 × 10 3 =

= 0.134 × 10 3

E A = 133.921 - 134 = 0.079

E R = E A 133.921 = 5.899 × 10 - 4

Passo 2

b

133 - 0.499 =

= 0.133 × 10 3 - 0.499 × 10 0 =

= 0.133 × 10 3 - 0.000499 × 10 3 =

= 0.132501 × 10 3 =

= 0.133 × 10 3

E A = 132.501 - 133 = 0.499

E R = E A 132.501 = 3 . 76601 × 10 - 3

Passo 3

c

121 - 0.327 - 119 =

= 0.121 × 10 3 - 0.327 × 10 0 - 0.119 × 10 3 =

= 0.121 × 10 3 - 0.000327 × 10 3 - 0.119 × 10 3 =

= 0.120673 × 10 3 - 0.119 × 10 3 =

= 0.121 × 10 3 - 0.119 × 10 3 =

= 0.002 × 10 3 =

= 0.2 × 10 1

E A = 1.673 - 2 = 0.327

E R = E A 1.673 = 0.19546

Passo 4

d

121 - 119 - 0.327 =

= 0.121 × 10 3 - 0.119 × 10 3 - 0.327 × 10 0 =

= 0.002 × 10 3 - 0.327 × 10 0 =

= 0.2 × 10 1 - 0.0327 × 10 1 =

= 0.1673 × 10 1 =

= 0.167 × 10 1

E A = 1.673 - 1.67 = 0.003

E R = E A 1.673 = 1.79319 × 10 - 3

Passo 5

e

13 14 - 6 7 2 e - 5.4 =

= 0.929 × 10 0 - 0.857 × 10 0 0.544 × 10 1 - 0.54 × 10 1 =

= 0.072 × 10 0 0.544 × 10 1 - 0.54 × 10 1 =

= 0.72 × 10 - 1 0.004 × 10 1 =

= 0.72 × 10 - 1 0 . 4 × 10 - 1 =

= 1.8 × 10 0 =

= 0.18 × 10 1

E A = 1.95354 - 1.8 = 0.15354

E R = E A 1.95354 = 0.078596

Passo 6

f

- 10 π + 6 e - 3 62 =

= - 0.314 × 10 2 + 0.163 × 10 2 - 0.484 × 10 - 1

= - 0.151 × 10 2 - 0.000484 × 10 2 =

= - 0 . 151484 × 10 2 =

= - 0 . 151 × 10 2

E A = - 15.15462 + 15.1 = 0.05462

E R = E A 15.15462 = 3.60418 × 10 - 3

Passo 7

g

2 9 ∙ 9 7 =

= 0.222 × 10 0 ∙ 0.129 × 10 1 =

= 0.028638 × 10 1 =

= 0 . 286 × 10 0

E A = 0.28571 4 - 0.286 = 0.2 86 × 10 - 3

E R = E A 0.28571 4 = 0.1 001 × 10 - 2

Passo 8

h

π - 22 7 1 17 =

= 0.314 × 10 1 - 0.314 × 10 1 0.588 × 10 - 1 =

= 0 0.588 × 10 - 1 =

= 0

E A = - 0.021496 - 0 = 0.021496

E R = E A 0.021496 = 1

Resposta

Exercícios de Livros Relacionados

Idem para u = 3 underset(_)(x) e w = underset(_)(x) + underset(_)(x) + underset(_)(x) .
É interessante observar que a adição em aritmética de ponto flutuante nem sempre é associativa. Prova-se que dados n números xl' x2, ... , xn representados exatamente, o limite do erro total devido ao
Verifique de alguma forma que, se r F tem representação finita na base 2 com k dígitos, ou seja, r F=( 0 .d 1 d 2 · · · d k ) 2 , então sua representação na base 10 é também finita com k dígitos.
Sejam x e y as representações de x e y obtidas por arredondamento em um computador. Deduza expressões de limitante de erro para mostrar que o limitante do erro relativo de u = 3 x y é menor que o de v
Supondo que x é representado num computador por x _ , onde x _ é obtido por arredondamento, obtenha os limites superiores para os erros relativos de u = 2 x _ e w = x _ + x _ .