Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Órbitas em Torno do Centro de Massa

Ver Teoria
Exercício 41235678910

Enunciado

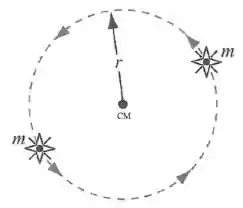
Uma estrela dupla consiste em duas estrelas de mesma massa m que executam órbitas circulares de mesmo raio r , mantendo-se sempre em pontos diametralmente opostos em relação ao centro de massa do sistema. A rapidez de cada estrela é

(A) G m r

(B) G m 2 r

(C) r G m

(D) 4 r G m

(E) G m 4 r

Passo 1

Nesse caso, temos duas estrelas orbitando uma junto com a outra. Elas orbitam a posição do centro de massa delas.

Cada uma exerce uma força gravitacional na outra capaz de mantê-las em órbita.

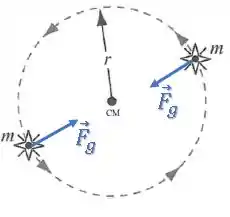
Queremos a velocidade orbital de cada estrela (a mesma para as duas).

Passo 2

Vamos igualar a força gravitacional à força centrípeta para obter uma expressão para a velocidade.

A força gravitacional é dada por:

F g = G M m d 2

A distância entre as estrelas é 2 r e as suas massa são iguais:

F g = G m m 2 r 2

Passo 3

Já a força centrípeta é dada por:

F c t p = m v 2 R

O raio da trajetória é r :

F c t p = m v 2 r

Passo 4

Igualando as duas, temos:

F g = F c t p

G m m 2 r 2 = m v 2 r

G m m 4 r 2 = m v 2 r

Cortando m e r :

G m 4 r = v 2

v = G m 4 r

Ficamos com a letra (E).

Resposta

Letra (E)

Exercícios de Livros Relacionados

12.54. Suponha que a órbita da Lua em torno da Terra seja circular. A partir do período orbital de 27,3 dias, calcule a distância da Lua ao centro da Terra. Suponha que o movimento da Lua seja determi
Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve: a. Redigir um problema realista para o qual esta seja a equação correta. b. Fa
Os astrônomos descobriram um sistema estelar binário com período de translação de 90 dias. O sistema consiste de duas estrelas de mesma massa, duas vezes maior que a do Sol, que giram como um haltere
O diâmetro angular aparente do Sol visto da Terra (ângulo subentendido pelo disco solar) é de 0,55 ° . Utilizando apenas estes dados, juntamente com o período da órbita da Terra em torno do Sol, aprox
O sistema binário de Plaskett consiste em duas estrelas que giram numa órbita circular em torno de um centro de massa a meio caminho entre elas. Essa afirmação implica que as massas das duas estrelas