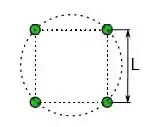
A figura ao lado mostra quatro estrelas de massa M formando um quadrado que gira em torno do centro de massa do sistema. O lado do quadrado possui comprimento L. Qual é o módulo da velocidade das estrelas? Expresse sua resposta em termos de L, M e da constante gravitacional G. Quando necessário, use
Passo 1
Como o problema é simétrico a velocidade e força resultantes em um estrela será em módulo igual as das outras.
Bem, como vamos descobrir a velocidade em um problema de gravitação? Pelo movimento circular que ela executa. Para que haja movimento circular deve-se ter força centrípeta. Como temos apenas força gravitacional. Temos que a força centrípeta é igual a força gravitacional resultante na direção do centro.
Então para descobrirmos a velocidade precisamos descobrir a força resultante em uma partícula.
Vamos aos desenhos das forças então:
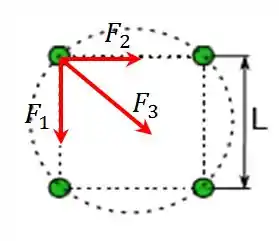
A força é
Na direção do eixo .
Já a força é na direção .
E por último a força três, para calcular essa força temos que primeiro descobrir qual é a distância entre as partículas. Bem como se trata de um quadrado, a distância será a diagonal do quadrado que vale .
Assim, a força será:
Essa é a única força que aponta para o centro. Então vamos ter que calcular qual é a resultante da força e depois somar com a força que já aponta para o centro.
Bem a resultante é
Somando com a resultante na direção do centro de massa é:
Voltando agora para a igualdade com a força centrípeta temos:
O raio é igual a metade da diagonal do quadrado, assim