Um satélite, em uma órbita elíptica de excentricidade , tem uma velocidade no apogeu, no perigeu, e nas extremidades do semieixo menor da sua órbita. Mostre que:
(a)
(b)
A excentricidade de uma elipse é definida como a razão entre a metade da distância focal e a metade da medida do eixo maior da elipse.
Passo 1
Essa é aquela famosa questão que o cara não sabe mais o que cobrar, aí pede uma demonstração hahaha.
Primeiro de tudo, como funciona uma órbita elíptica?
Basicamente, uma elípse tem dois pontos chamados focos:
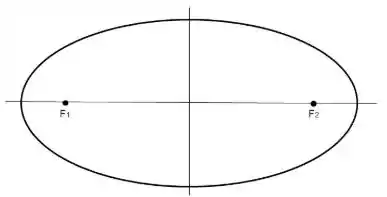
O corpo orbitado, tipo o que o Sol é para a Terra, fica em um dos focos da elípse, enquanto o corpo que orbita realiza o trajeto da elipse:
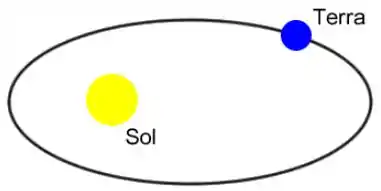
Beleza,mas vamos ao segundo ponto...
Que negócio de apogeu e perigeu é esse??
Ah, o perigeu é o ponto que a “Terra” (corpo que orbita) chega mais próximo do ”Sol” (corpo orbitado).
Enquanto o apogeu é o ponto que a “Terra” (corpo que orbita) fica mais afastada do ”Sol” (corpo orbitado).
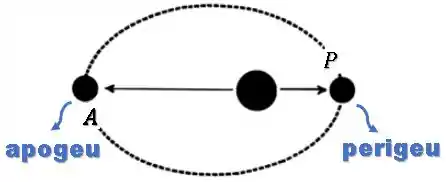
Lembra assim:
Show, mas como vamos relacionar os velocidades nos pontos e ?
Como a força gravitacional não gera torque, o momento angular se conserva:
O momento angular é dado pelo produto vetorial entre o raio e o momento linear :
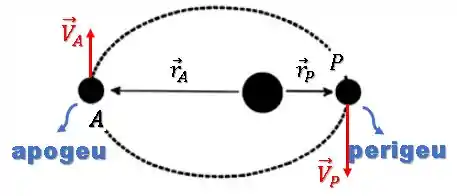
Como os vetores e são perpendiculares no ponto e no ponto , seus momentos angulares terão como módulo:
Então, conservando o momento angular, temos:
Então, podemos relacionar as velocidades a partir dos raios:
Agora, só falta relacionar os raios.
Só... rs.
Passo 2
Para achar as relações entre os raios, dá uma olhada na elipse:
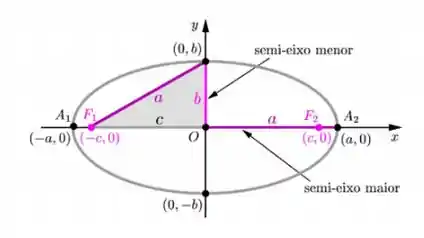
Tanto a distância quanto a distância são iguais ao raio do perigeu (perigeu). Enquanto a distância entre e é igual a . Além disso, eixo maior vale .
Então:
Essa é nossa primeira relação.
Passo 3
Vamos achar uma relação envolvendo o agora:
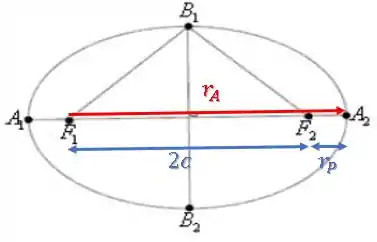
Como achamos no Passo 2 que:
Substituindo isso, temos:
Agora é só substituir os raios.
Passo 4
Substituindo os raios na expressão das velocidades, temos:
Passo 5
Falta um detalhe... relacionar com a excentricidade .
A excentricidade da elipse é dada pela metade da distância entre os focos dividida pela metade do comprimento do eixo maior :
Passo 6
Então, se dividirmos a nossa expressão por :
Então, achamos que:
Letra (a) demonstrada!

Passo 7
Para demonstrar a letra (b), vamos fazer algo bem parecido.
O ponto onde a velocidade é (extremidade do eixo menor) é esse aqui:
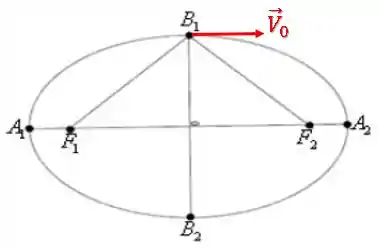
Como queremos relacionar com , vamos conservar o momento angular entre eles:
Já vimos que o momento angular no apogeu será:
Porém no ponto onde a velocidade é , é diferente.
Seu momento angular será:
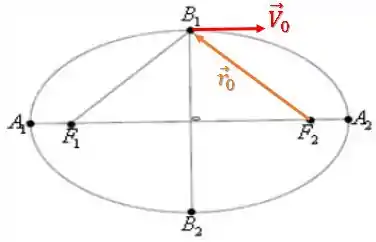
Para o produto vetorial:
Podemos pegar a distância perpendicular à velocidade entre e o ponto:
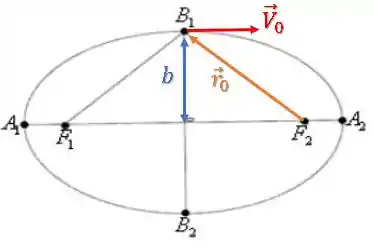
Então, o momento angular será:
Passo 8
Conservando o momento angular, temos:
Substituindo o valor de , temos:
Mas quem é esse ?
Podemos aplicar um Pitágoras alí no triângulo retângulo:
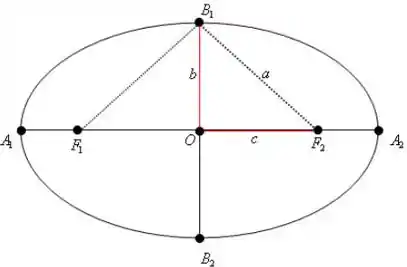
Substituindo o valor de , temos:
Passo 9
Vamos manipular isso um pouquinho:
Pode parecer meio doido, mas a gente está olhando para a resposta e tentando fazer aparecer aquele resultado, então é só um pouquinho menos doido.
Vamos abrir o produto notável no denominador:
Agora, vamos escrever o numerador como um produto de raizes:
Ahh, encontramos exatamente aquela mesma expressão que para a letra (a):
Substituindo isso dentro dos parênteses, temos:
Demonstramos a letra (b) também.

Resposta
Ei, a resposta está no passo a passo :)