Considere duas estrelas de nêutrons, de mesma massa , que formam um sistema binário no qual ambas giram em torno do centro de massa do sistema. Suponha também que as estrelas estão sempre em pontos opostos de uma mesma órbita circular de raio . A velocidade orbital de cada estrela em termos de , , e é:
(A)
(B)
(C)
(D)
(E)
Passo 1
Temos dois planetas em uma trajetória circular:
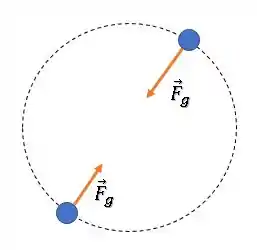
A força gravitacional entre eles os mantêm nessa trajetória circular.
A força gravitacional entre eles é dada por:
Como a massa de ambos os planetas é :
Além disso, a distância entre eles é duas vezes o raio da trajetória circular:
Então, temos:
Passo 2
Já que eles realizam uma trajetória circular, podemos igualar a força à expressão da força centripeta:
Então, temos que:
Resposta
Letra (E)
Exercícios de Livros Relacionados
12.54. Suponha que a órbita da Lua em torno da Terra seja circular. A partir do período orbital de 27,3 dias, calcule a distância da Lua ao centro da Terra. Suponha que o movimento da Lua seja determi
Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve: a. Redigir um problema realista para o qual esta seja a equação correta. b. Fa
Os astrônomos descobriram um sistema estelar binário com período de translação de 90 dias. O sistema consiste de duas estrelas de mesma massa, duas vezes maior que a do Sol, que giram como um haltere
O diâmetro angular aparente do Sol visto da Terra (ângulo subentendido pelo disco solar) é de 0,55 ° . Utilizando apenas estes dados, juntamente com o período da órbita da Terra em torno do Sol, aprox
O sistema binário de Plaskett consiste em duas estrelas que giram numa órbita circular em torno de um centro de massa a meio caminho entre elas. Essa afirmação implica que as massas das duas estrelas