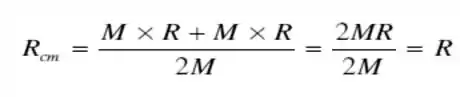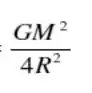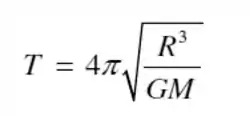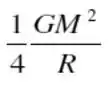Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Órbitas em Torno do Centro de Massa

Ver Teoria
Exercício 81234567910

Enunciado

Passo 1

Para calcular o centro de massa vamos usar as posições e as massas das estrelas

R C m = M x R + M x R 2 M = R

Passo 2

A força gravitacional vamos usar a lei da gravitação

F = G M M 2 R 2

F = G M 2 4 R 2

Passo 3

Como já descobrimos o raio da órbita das estrelas R e a força que elas estão sofrendo, então conseguimos achar a velocidade iguala a força centrípeta

F = F c p

G M 2 4 R 2 = M V 2 R

Isolando o V conseguimos achar o valor dele direitinho

V = G M 4 R

Agora que já descobrimos o valor da velocidade conseguimos também descobrir o valor do período

v = 2 π R T

T = 2 π R v

Substituindo o valor da velocidade pra achar finalmente o período orbital temos

T = 4 π R 3 G M

Passo 4

A energia necessária para separa as estrelas a uma distância infinita é dada pela diferença entre a energia mecânica total da estrela binária em órbita, E b , e a energia mecânica total, E i n f i n i t o , quando as estrelas estão infinitamente separadas. A energia mecânica da órbita é:

E b = K 1 + K 2 + U = 2 m v 2 2 - G m 2 2 R

Substituindo os valores que nós já conhecemos ficamos com

E b = G m 2 4 R - G m 2 2 R = - 1 4 G m 2 R

A energia mecânica das estrelas no infinito é:

E i n f i n i t o = K 1 i n f i n i t o + K 2 i n f i n i t o + U i n f i n i t o = 0

W = E i n f i n i t o - E b = 1 4 G m 2 R

Resposta

Exercícios de Livros Relacionados

12.54. Suponha que a órbita da Lua em torno da Terra seja circular. A partir do período orbital de 27,3 dias, calcule a distância da Lua ao centro da Terra. Suponha que o movimento da Lua seja determi
Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve: a. Redigir um problema realista para o qual esta seja a equação correta. b. Fa
Os astrônomos descobriram um sistema estelar binário com período de translação de 90 dias. O sistema consiste de duas estrelas de mesma massa, duas vezes maior que a do Sol, que giram como um haltere
O diâmetro angular aparente do Sol visto da Terra (ângulo subentendido pelo disco solar) é de 0,55 ° . Utilizando apenas estes dados, juntamente com o período da órbita da Terra em torno do Sol, aprox
O sistema binário de Plaskett consiste em duas estrelas que giram numa órbita circular em torno de um centro de massa a meio caminho entre elas. Essa afirmação implica que as massas das duas estrelas