Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Órbitas em Torno do Centro de Massa

Ver Teoria
Exercício 12345678910

Enunciado

Em um sistema binário de estrelas, duas estrelas descrevem órbitas circulares em torno de seu centro de massa comum. Se as estrelas possuem massas m 1 e m 2 e estão separadas por uma distância r , mostre que o período de rotação está relacionado a r através de:

T 2 = 4 π 2 r 3 G m 1 + m 2

Passo 1

Tá, nesse problema nós temos duas estrelas descrevendo órbitas circulares em torno do seu centro de massa comum.

Vamos considerar que a estrela de massa m 1 dista r 1 do centro de massa e a outra dista r 2 .

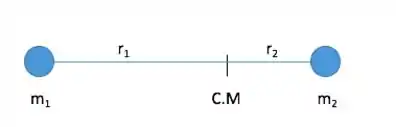
Logo, temos que:

r = r 1 + r 2

Pela fórmula do centro de massa, temos:

m 1 r 1 = m 2 r 2 → m 1 r - r 2 = m 2 r 2 → r 2 = r m 1 m 1 + m 2

Vamos deixar esse resultado guardado por um tempo.

Passo 2

-

Vamos agora calcular a força gravitacional que age na massa m 1 (que é a mesma que age na massa m 2 ):

F = G m 1 m 2 r 1 + r 2 2

Essa força também é centrípeta. Logo:

F = G m 1 m 2 r 1 + r 2 2 = m 2 ω 2 r 2 → ω 2 = G m 1 r 2 r 1 + r 2 2 = G m 1 r 2 r 2

Substituindo a expressão que obtivemos no passo 1 nessa equação, teremos:

ω 2 = G m 1 ( m 1 + m 2 ) r m 1 r 2 = G m 1 + m 2 r 3

Mas também sabemos que:

ω = 2 π T → T 2 = 4 π 2 ω 2

Logo:

T 2 = 4 π 2 r 3 G m 1 + m 2

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

12.54. Suponha que a órbita da Lua em torno da Terra seja circular. A partir do período orbital de 27,3 dias, calcule a distância da Lua ao centro da Terra. Suponha que o movimento da Lua seja determi
Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve: a. Redigir um problema realista para o qual esta seja a equação correta. b. Fa
Os astrônomos descobriram um sistema estelar binário com período de translação de 90 dias. O sistema consiste de duas estrelas de mesma massa, duas vezes maior que a do Sol, que giram como um haltere
O diâmetro angular aparente do Sol visto da Terra (ângulo subentendido pelo disco solar) é de 0,55 ° . Utilizando apenas estes dados, juntamente com o período da órbita da Terra em torno do Sol, aprox
O sistema binário de Plaskett consiste em duas estrelas que giram numa órbita circular em torno de um centro de massa a meio caminho entre elas. Essa afirmação implica que as massas das duas estrelas