(A) A Lua é atraída pela força gravitacional da Terra. Por que ela não se choca contra a Terra?

Em um movimento circular uniforme, a partícula realiza uma trajetória circular com velocidade constante. Assim, a única força que atua sobre ela é a força centrípeta apontando para o centro da trajetória.

Como a força é perpendicular à velocidade da partícula, ela apenas altera a direção da velocidade e não seu módulo (valor) em si.

Mas o ponto é...

Para que a partícula realize um movimento circular de raio com uma certa velocidade :

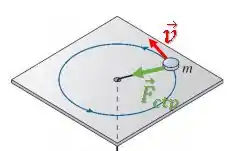
a força atuando sobre ela deve ter um valor específico, esse valor específico é calculado pela expressão da força centrípeta:

Então, se a força a força atuando sobre a partícula for menor que esse valor da , a partícula tende a sair da trajetória circular “para fora da curva”:

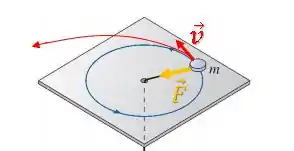
Enquanto isso, se a força atuando sobre a partícula for maior que esse valor da , a partícula tende a sair da trajetória circular “para dentro da curva”:

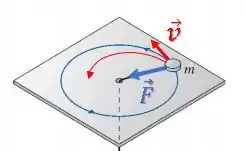
Fazendo uma analogia à Lua orbitando a Terra, a força atuando sobre a Lua é a força gravitacional , que varia conforme a distância em que a Lua se encontra da Terra.

Porém, para uma determinada velocidade e uma distância na qual a Lua se encontra, a força gravitacional apresenta exatamente aquele valor específico da :

Por isso, a Lua está recebendo uma força com intensidade suficiente para manter sua trajetória circular e por isso ela não vai se aproximando ou se afastando da Terra. Isso que significa estar em órbita.