Seja
O valor de para que se tenha é:
Passo 1
Vamos lá!! A carinha da função exponencial e queremos encontrar o valor de de forma que , certo? Como podemos fazer isso??

Primeiro passo é substituir a função
Na igualdade
Beleza?! Assim,
Passo 2
Se você reparar, todos os termos do lado esquerdo da equação tem o , então vamos colocá-lo em evidência, beleza?!
Tá... mas como podemos tirar esses expoentes negativos??

Bom, podemos inverter o sinal do expoente transformando-o em uma fração! Vai ficar assim:
Beleza?!
Passo 3
Fazendo as continhas, temos
Agora podemos fazer o MMC entre os denominadores, assim

Continuando as continhas, temos
![]()
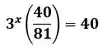
Passo 4
Agora passaremos o para o lado direito da equação. Para isso, precisaremos inverter o numerador e o denominador:
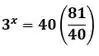
OPA! Podemos simplificar e cortar o !!
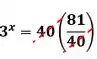
Assim, ficamos com
![]()
Passo 5
Ó, do lado esquerdo da equação temos um número com base , certo? Vamos tentar escrever o lado direito da equação como um número de base também???

Se você reparar, podemos reescrever o número como
![]()
Assim, ficamos com
![]()
Dessa forma conseguimos encontrar o valor de :
![]()