Determine e esboce o gráfico da função
Passo 1
Nesse caso, temos que
Assim, o gráfico de vai ser algo de dimensão , que nada mais é que uma superfície.
Passo 2
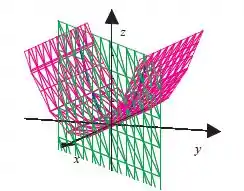
Agora vamos descobrir que superfície é essa. Como o gráfico é o conjunto de pontos ordenados , temos:
Agora, para esboçar esse gráfico, temos que ver que
Assim, o gráfico será a interseção do plano
Com o cilindro
Ou
Que dá no mesmo já que .
Passo 3
Portanto, temos uma curva no espaço (lembra que eram 3 dimensões?)
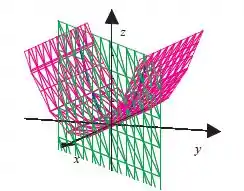
Resposta
Exercícios de Livros Relacionados
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro t cresce. r t = t ,2 - t ,2 t
Encontre uma equação vetorial e equações paramétricas para o segmento de reta que liga P e Q. P 0 , - 1,1 , Q 1 2 , 1 3 , 1 4
Desenhe as projeções da curva nos três planos coordenados. Use essas projeções para ajudá-lo a esboçar a curva. r t = t , sen t , 2c o st
Determine a função vetorial que representa a curva obtida pela interseção das duas superfícies. z = x 2 - y 2 x 2 + y 2 = 1
(a) Esboce o gráfico da curva plana com a equação vetorial dada.(b) Encontre r ’ ( t ) (c) Esboce o vetor posição r ( t ) e o vetor tangente r ’ ( t ) para o valor dado de t . r t = t 2 , t 3 ,t = 1