Exercícios Resolvidos de Gráfico de Funções Vetoriais

Exercício 10 1 2 3 4 5 6 7 8 9 11 12 13 14

Enunciado

UFU, Sem Campus, Cálculo 3, Listas de Cálculo 3 - Profª Lúcia - Lista de Integral de Linha - 2023.1, Questão 3d

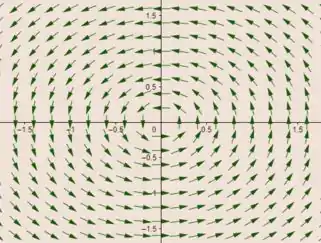
3. Faça a representação geométrica dos seguintes campos vetoriais :

d)

Passo 1

Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉

Esboçar um campo vetorial envolve representar visualmente a direção e a intensidade de um conjunto de vetores em pontos específicos dentro de uma região ou espaço.

Porém, nem sempre os vetores serão iguais em todo o espaço, portanto, conforme e variam, o campo vetorial pode apontar para diferentes sentidos e com diferentes intensidades...

Parece complicado? 👀

Passo 2

Nesse caso o campo vetorial é dado por

Para poder visualizar como os vetores desse campo podemos aplicar a parametrização por coordenadas polares fazendo e

A partir dessa função podemos perceber que os vetores desse campo apontam tangencialmente à circunferências de raio ...

Esboçando o campo vetorial , temos

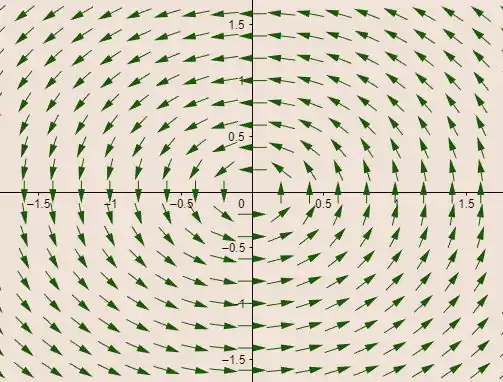
Pegou o esquema? Responde Aí! 😁

Resposta

Exercícios de Livros Relacionados

Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro t cresce. r t = t ,2 - t ,2 t

Encontre uma equação vetorial e equações paramétricas para o segmento de reta que liga P e Q. P 0 , - 1,1 , Q 1 2 , 1 3 , 1 4

Desenhe as projeções da curva nos três planos coordenados. Use essas projeções para ajudá-lo a esboçar a curva. r t = t , sen ⁡ t , 2c o st

Determine a função vetorial que representa a curva obtida pela interseção das duas superfícies. z = x 2 - y 2 x 2 + y 2 = 1

(a) Esboce o gráfico da curva plana com a equação vetorial dada.(b) Encontre r ’ ( t ) (c) Esboce o vetor posição r ( t ) e o vetor tangente r ’ ( t ) para o valor dado de t . r t = t 2 , t 3 ,t = 1