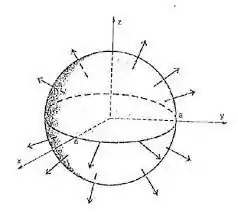
5. Seja , onde . Desenhe com ; , , .
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nesse problema foi dada uma função de um campo vetorial e nosso objetivo é esboçar a parte do campo que está sob a circunferência com , e ...
Tem ideia de como fazer isso? 🤔
Para esboçar um campo vetorial, precisamos entender como os vetores desse campo se comportam no espaço...
Nesse caso, como estamos interessados apenas nos vetores contidos na esfera, podemos aplicar a parametrização por coordenadas esféricas na função e ver como o campo se comporta nesse domínio.
Sacou? Bora começar! 👀
Passo 2
Mas primeiro de tudo temos que descobrir qual é o campo .
Foi dito que onde
Calculando o gradiente de , temos
Portanto, temos que
Aplicando a parametrização por coordenadas esféricas sabendo que , temos
A partir dessa parametrização, podemos perceber que os vetores do campo apontam para o sentido radial à esfera... ou seja, os vetores de são normais à superfície esférica.
Esboçando o campo , teremos algo próximo a
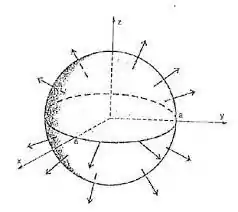
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta