UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo de Várias Variáveis - Lista 2 - Integral de Linha, Questão 2.1.1f
Esboce o gráfico de cada curva abaixo, indicando a orientação positiva.
(f)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente esboçar a curva da equação paramétrica no intervalo . Pra isso, nós precisamos lembrar que nas curvas parametrizadas e são dadas em função de uma terceira variável (denominada parâmetro), que de forma geral pode ser definida por:
Onde a curva tem ponto inicial e ponto final . Então, cada valor de fornece um ponto na curva, no plano cartesiano. Sendo assim, o que nós vamos fazer é atribuir diferentes valores para , dentro do intervalo dado, marcar os pontos correspondentes no gráfico e unir esses pontos. No sentido de crescimento do parâmetro , vamos ter a orientação positiva da nossa curva.
Vamos lá!
Passo 2
Para , vamos ter:
Então, nós temos uma curva no espaço tridimensional . Considerando o intervalo , podemos definir os pontos:
Marcando esses pontos no gráfico , vamos ter a hélice:
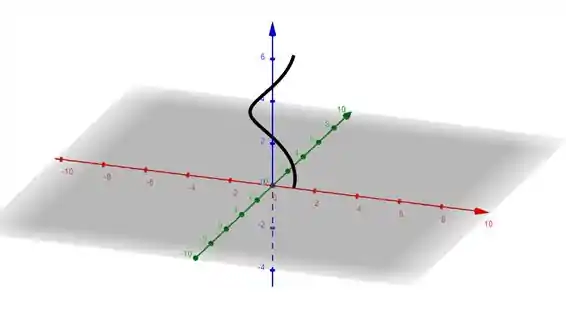
Como a gente começa marcando o ponto e termina marcando o ponto , essa é a nossa orientação positiva, que é o sentido de crescimento do parâmetro .
Valeu, galera! Até a próxima! 😉