Exercícios Resolvidos de Gráfico de Funções Vetoriais

Exercício 12 1 2 3 4 5 6 7 8 9 10 11 13 14

Enunciado

UFU, Sem Campus, Cálculo 3, Listas de Cálculo 3 - Profª Lúcia - Lista de Integral de Linha - 2023.1, Questão 4

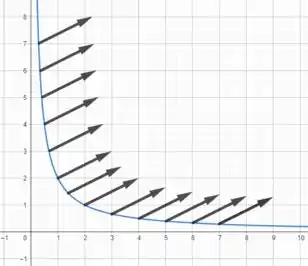
4. Seja . Desenhe nos pontos da hipérbole , com

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema foi dada uma função de um campo vetorial e nosso objetivo é esboçar a parte do campo que está sob a hipérbole com ...

Tem ideia de como fazer isso? 🤔

Para esboçar um campo vetorial, precisamos entender como os vetores desse campo se comportam no plano...

Nesse caso, como estamos interessados apenas nos vetores acima da hipérbole, podemos aplicar a equação da hipérbole na função e ver como o campo se comporta nesse domínio.

Sacou? Bora começar! 👀

Passo 2

A hipérbole é dada por

Podemos isolar como

Substituindo na função ...

Dessa forma, vemos que nos pontos acima da hipérbole, os vetores do campo são idênticos e iguais a ...

Esboçando esses vetores no plano, temos

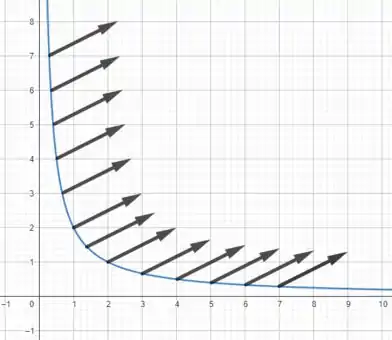
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

Exercícios de Livros Relacionados

Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro t cresce. r t = t ,2 - t ,2 t

Encontre uma equação vetorial e equações paramétricas para o segmento de reta que liga P e Q. P 0 , - 1,1 , Q 1 2 , 1 3 , 1 4

Desenhe as projeções da curva nos três planos coordenados. Use essas projeções para ajudá-lo a esboçar a curva. r t = t , sen ⁡ t , 2c o st

Determine a função vetorial que representa a curva obtida pela interseção das duas superfícies. z = x 2 - y 2 x 2 + y 2 = 1

(a) Esboce o gráfico da curva plana com a equação vetorial dada.(b) Encontre r ’ ( t ) (c) Esboce o vetor posição r ( t ) e o vetor tangente r ’ ( t ) para o valor dado de t . r t = t 2 , t 3 ,t = 1