Considere as transformações lineares A, B, C: cujas matrizes na base canônica são, respectivamente:
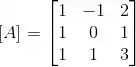
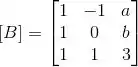
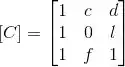
(a) Determine uma base do espaço imagem de A (ou, equivalentemente, o espaço coluna da matriz ).
(b) Determine a e b para que a imagem de B (ou, equivalentemente, o espaço coluna da matriz ) seja um plano.
(c) Determine c, d, l e f para que a imagem de C (ou, equivalentemente, o espaço coluna da matriz ) seja uma reta.
Passo 1
(a) A imagem ou o espaço coluna da matriz é o espaço gerado pelas colunas.
No caso da matriz A, vai ser o espaço gerado pelos vetores e
Vamos ver se esses 3 vetores são LI. Se forem, já formam uma base para esse espaço.
Sabemos que um conjunto de vetores é LI se a única combinação linear entre eles que gera o vetor nulo é a combinação linear trivial (todos os coeficientes iguais a zero).
Montando essa CL:
Ficamos com o sistema:
Da segunda equação:
Substituindo na primeira:
Substituindo na terceira:
Ou seja:
Logo:
E os três vetores são LI.
Logo já formam uma base para a imagem da matriz A.
Passo 2
(b) Queremos que a imagem seja um plano.
Lembra que o plano é um espaço de dimensão 2?
Isso significa que a base da imagem de B tem que ser um conjunto com dois vetores.
Como a base tem que ser um conjunto LI, concluímos que um dos vetores das colunas é combinação linear dos outros.
Sabendo disso vamos dar uma olhada na matriz B:
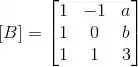
Vemos que as duas primeiras colunas são LI (uma não é múltipla da outra).
Logo, a única opção que sobra é a terceira coluna ser combinação linear das duas primeiras:
Já temos pela segunda equação que:
Substituindo na primeira:
Substituindo na última:
Substituindo na equação :
Então, quaisquer valores de a e b que satisfaçam essa relação faz com que a imagem seja um plano (tenha dimensão 2).
Podemos fazer por exemplo:
e
Passo 3
(c) Agora queremos que a imagem seja uma reta.
Lembra que a reta é um espaço de dimensão 1?
Isso significa que a base da imagem de C tem que ser um conjunto com um vetor.
Como a base tem que ser um conjunto LI, concluímos que dois vetores das colunas são combinação linear de outro, ou seja, todos os vetores das colunas são múltiplos.
Sabendo disso vamos dar uma olhada na matriz C:
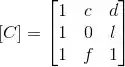
Queremos então que:
Resposta
(a)
(b) Quaisquer valores de a e b satisfazendo .
(c) e