Considere o plano de equação cartesiana:
e as transformações lineares P de projeção ortogonal no plano e E de espelhamento em relação ao plano .
(a) Determine a matriz de P na base canônica.
(b) Determine a matriz de E na base canônica.
(c) Determine a matriz da composição na base canônica.
(d) Encontre um plano (em equação cartesiana) tal que seja uma reta.
Passo 1
Antes de resolver essa questão, vamos começar definindo uma base para o formada por um vetor normal ao plano e por dois vetores do plano.
O plano dado é
Sabemos que os coeficientes dessa equação representam um vetor normal ao plano .
Então:
Agora precisamos achar uma base para o plano.
Os vetores do plano são vetores satisfazendo:
Logo:
Então uma base para o plano pode ser:
E uma base pra é:
Agora vamos lembrar que:
- A projeção ortogonal em de um vetor que pertence a dá o próprio vetor.
- A projeção ortogonal em de um vetor perpendicular a dá o vetor nulo.
- A reflexão em torno de de um vetor que pertence a dá o próprio vetor.
- A reflexão em torno de de um vetor perpendicular a dá menos esse vetor.
Agora que fizemos isso vamos começar a resolver a questão!
Passo 2
(a) Como queremos achar a matriz que representa a TL, vamos aplicar a transformação (que é a projeção) nos vetores da base.
Lembrando que a base que achamos é:
Temos:
Mas queremos a matriz na base canônica, então não podemos parar aqui.
Vamos escrever os vetores da base canônica do a partir dos vetores da base
Vamos começar com o vetor
Da última equação:
Da primeira:
Substituindo esses valores de x e y na segunda equação:
Logo:
Então:
Agora vamos para o vetor
Da terceira equação:
Da primeira equação:
Substituindo na equação do meio:
Então:
E:
Por último, vamos para o vetor
Da primeira equação:
Substituindo na segunda:
Somando essa equação com a terceira:
Então:
E:
Mas por que fizemos tudo isso mesmo??
Porque queremos a matriz que representa a transformação de projeção na base canônica.
E só tínhamos como saber o que acontece com os vetores da base que achamos.
Mas agora temos o seguinte:
Aplicando P dos dois lados:
Mas P é linear, então:
Mas vimos que:
Logo:
E essa é a primeira coluna da matriz P na base canônica!
Agora vamos fazer a mesma coisa para o vetor
Essa é a segunda coluna da matriz P na base canônica.
Por último, vamos para o vetor
E essa é a terceira coluna da matriz P na base canônica.
Então a matriz P é:

Passo 3
(b) Para a reflexão, temos:
Mas:
Aplicando E dos dois lados:
Mas E é linear, então:
Logo:
E essa é a primeira coluna da matriz E na base canônica!
Vamos fazer a mesma coisa para o vetor
Essa é a segunda coluna da matriz E na base canônica.
Por último, vamos para o vetor
E essa é a terceira coluna da matriz E na base canônica.
Então a matriz E é:
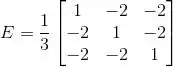
Passo 4
(c) Observe que:
Ou seja, e P são iguais quando aplicadas aos vetores da base, portanto as matrizes que as representam são iguais.
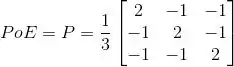
Passo 5
(d) Sabemos que o plano tem dimensão 2, então tem dois vetores na sua base.
Vamos chamar de os vetores da base do plano
Se é um vetor do plano pedido, então:
E:
Mas como , que é uma reta.
Então P(w) só é gerado por 1 vetor.
Isso significa que ou ou
Então um desses vetores é o vetor pois vimos antes que
Vamos dizer que esse vetor seja o
Portanto, qualquer plano que contém o vetor satisfaz a condição do enunciado.
Podemos dar como resposta por exemplo o plano de equação ou ou , e assim por diante.
Resposta
(a) 
(b) 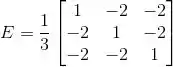
(c) 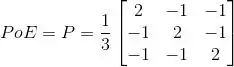
(d) Qualquer plano que contém o vetor , por exemplo o plano