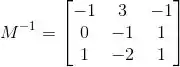Considere a matriz
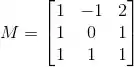
e a transformação linear cuja matriz na base canônica é M.
(a) Determine a matriz inversa de M.
Passo 1
(a) Vamos escalonar completamente a matriz M com a identidade do lado direito.
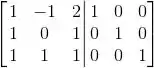
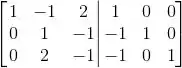
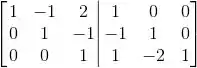
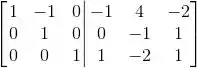
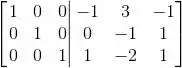
Então:
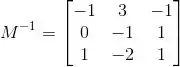
Resposta
(a)
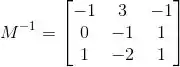
Considere a matriz
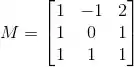
e a transformação linear cuja matriz na base canônica é M.
(a) Determine a matriz inversa de M.
(a) Vamos escalonar completamente a matriz M com a identidade do lado direito.

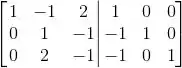

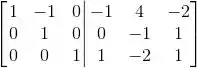
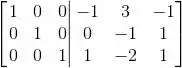
Então:
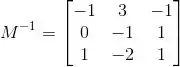
(a)