P1 de Cálculo 1 da USP - 2020
Cálculo 1 - USP
Considere a função dada por . A soma dos valores máximo e mínimo de em é igual a:
Ver solução completaOs ponteiros de um relógio mede 4 cm e 8 cm e movem-se, cada um com sua velocidade, que é constante. Quando o relógio marca exatamente duas horas, a distância entre as pontas dos ponteiros está diminuindo a uma taxa de:
Ver solução completaEstude a função dada por
1) Estude o crescimento de , determinando os pontos de máximo e de mínimo locais e globais de , se existirem.
2) Estude a concavidade de
3) Determine as assíntotas do gráfico de , se existirem.
4) Faça um esboço do gráfico de
Ver solução completaSeja , onde , , são constantes reais. Considere as seguintes afirmações:
- Existe tal que .
- possui ao menos um ponto crítico.
- possui exatamente um ponto de inflexão.
- Se então é injetora.
É sempre correto somente o que se afirma em:
- , e
- e
- e
- , e
- e
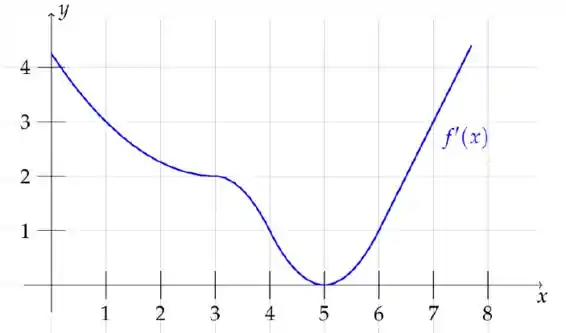
Seja uma função derivável até segunda ordem. O gráfico de sua derivada está ilustrado abaixo. Assinale a afirmação FALSA
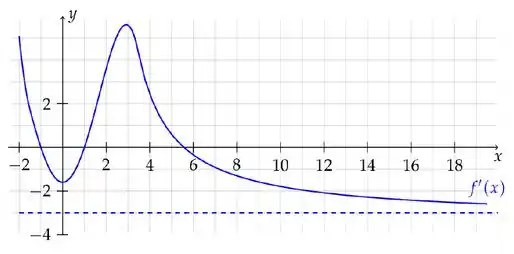
a) tem um único ponto de mínimo local, que ocorrem em
b) A equação tem pelo menos duas soluções reais distintas.
c) em
d) Pode ocorrer de a equação ter exatamente uma solução real.
e) tem mínimo global.
Ver solução completaAssinale somente as alternativas com afirmações corretas.
(Haverá desconto na nota desta questão caso alternativas incorretas sejam assinaladas.)
Escolha uma ou mais:
a) Se é uma função qualquer tal que , então existe tal que
b) Se e são função deriváveis definidas em e se em , então em
c) Se é uma função que admite derivada até segunda ordem em toda a reta, tal que e , então
d) Se e são polinômios, tais que grau(), então possui assíntotas vertical, ou seja, existe tal que ou
e) Se é uma função derivável até segunda ordem tal que tem duas soluções reais distintas, então tem algum ponto de extremo (máxima ou mínimo) local.
f) Se é uma função tal que para todo então .
Ver solução completa