Seja , onde , , são constantes reais. Considere as seguintes afirmações:
- Existe tal que .
- possui ao menos um ponto crítico.
- possui exatamente um ponto de inflexão.
- Se então é injetora.
É sempre correto somente o que se afirma em:
- , e
- e
- e
- , e
- e
Passo 1
Bom, vamos analisar então essa primeira afirmação: Existe tal que
Isso nos diz basicamente que a nossa função, em algum momento vai se encontrar com a função
Como estamos trabalhando com uma equação do terceiro grau, é interessante lembrar da carinha dele.
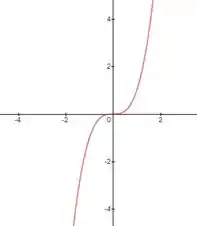
Como sabemos que ele vai desde menos infinito, até mais infinito, podemos afirmar que certamente em algum momento ele se cruza com a função
Passo 2
A segunda afirmação nos diz que possui ao menos um ponto crítico. Isso não necessariamente é verdade.
Os pontos críticos são aqueles onde a primeira derivada da função seja igual a zero. Observe que como temos uma equação do terceiro grau, sua primeira derivada vai nos levar a uma equação do segundo grau, certo?
Ou seja, estamos nos referindo ao ponto onde a equação do segundo grau é igual a zero. Uma equação do segundo grau não necessariamente tem que tem um
Exemplo: . Olha o gráfico dela
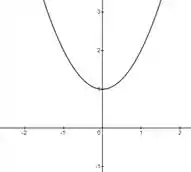
Em nenhum momento ela cruza o eixo x, ou seja, em nenhum momento ela é igual a zero.
Passo 3
Próxima afirmação que temos é possui exatamente um ponto de inflexão. Os pontos de inflexão são encontrados quando a segunda derivada é igual a zero. Vamos conferir isso então:
Opa, sabemos então que o único ponto de inflexão é em
Passo 4
Por último vamos avaliar se então a será injetora ou não.
Antes de mais nada, precisamos lembrar que a função é chamada de injetora qundo, se
Na equação do terceiro grau termos justamente essa relação, onde para ser injetora.
Ou seja, a relação entre o termo que multiplica o (no caso o ) e o que multiplica o (o ) tem que respeitar essa relação.
Caso seja maior do que , a função passa a ter um máximos e um mínimo, como nesse exemplo
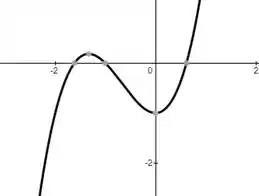
Passando a ser sobrejetora.
Resposta
, e