Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 241234567891011121314151617181920212223252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Os ponteiros de um relógio mede 4 cm e 8 cm e movem-se, cada um com sua velocidade, que é constante. Quando o relógio marca exatamente duas horas, a distância entre as pontas dos ponteiros está diminuindo a uma taxa de:

Passo 1

Bom, pra resolvermos algo de taxa relacionada, precisamos da equação que relaciona nossos parâmetros, certo?

Observa que o enunciado nos pergunta a taxa no momento em que o relógio marca 2h, ou seja

Isso nos da um intervalo de 60 ° .

Sou muito grato a minha mãe por ter me ensinado a ler relógio analógico agora!! Se isso fosse sua prova e você não sabia como funciona um relógio desses, só chora.

Passo 2

Bom, agora precisamos relacionar a distancia entre da ponta dos ponteiros

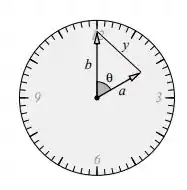
Chamaremos de y a distancia entre as pontas dos ponteiros, e θ o ângulo existente entre eles.

Relacionando esse parâmetros, podemos usar a regra dos cossenos

y = a 2 + b 2 - 2 a b c o s θ

Passo 3

Vamos ver então como que essa distância está variando, já que é o que o enunciado está nos pedindo.

y ' = 1 2 a 2 + b 2 - 2 a b   c o s θ × - - 2 a b s e n θ θ '

Beleza então, nosso problema agora se reduz a encontrar a velocidade com o θ varia.

Precisamos saber a velocidade com que os ponteiros se movimentam. Se você estiver ligado nos paranauê dos relógios analógicos, tem que se ligar que o ponteiro da hora anda 1h (ou seja, 1 / 12 do relógio) quando o ponteido dos minutos dá um volta completa.

Ou seja

ω h = ω m 12

Temos ainda que o ponteiro do minuto dura 60 minutos pra dar a volta completa no relógio ( 2 π ), logo

ω m = 2 π 60 = π 30   r a d / m i n

Então pra a velocidade angular do ponteiro da hora teremos

ω h = π 360   r a d / m i n

Ou seja, sabemos que θ varia a ma velocidade igual a

θ ' = π 30 - π 360 = 11 π 360

Passo 4

Podemos então voltar pra nossa derivada la em cima

y ' = 1 2 a 2 + b 2 - 2 a b   c o s θ × - - 2 a b s e n θ θ '

y ' = 1 2 4 2 + 8 2 - 64   c o s 60 × 64 s e n 60 11 π 360

y ' = 1 2 16 + 64 - 64 2 × 64 3 2 × 11 π 360

y ' = 1 2 48 × 704 π 3 720

y ' = 22 π 3 45 2 4 × 3

y ' = 22 π 3 45 × 2 2 3

y ' = 22 π 180

y ' = 11 π 90   c m / m i n

Resposta

11 π 90   c m / m i n

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s