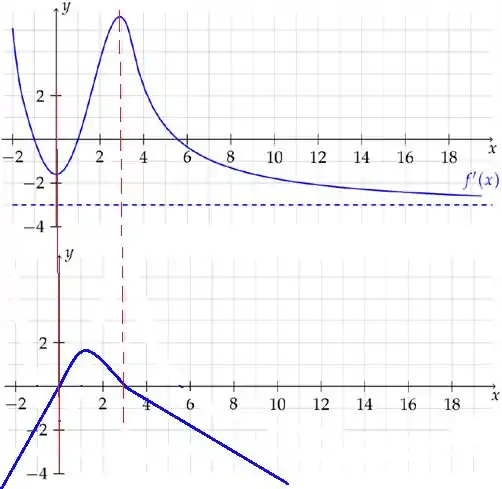
Seja uma função derivável até segunda ordem. O gráfico de sua derivada está ilustrado abaixo. Assinale a afirmação FALSA
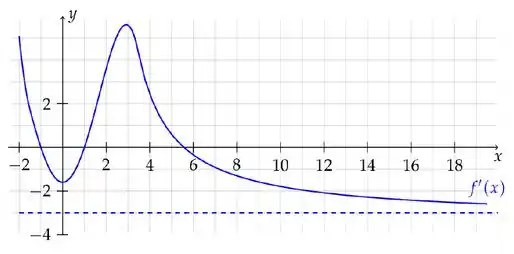
a) tem um único ponto de mínimo local, que ocorrem em
b) A equação tem pelo menos duas soluções reais distintas.
c) em
d) Pode ocorrer de a equação ter exatamente uma solução real.
e) tem mínimo global.
Passo 1
a) Verdadeiro! Lembra que quando a primeira derivada é igual a zero nos mostra os pontos de máximo e mínimo? Lembra ainda que quando ela é negativaa significa que sua função estava decrescendo e quando ela era positiva ela estava crescendo? Então...
Observando o gráfico ali notamos que quando a função é menos que 1 ela é negativa e vira positiva, logo a função vinha decrescente, chega no mínimo e passa a ser crescente.
Passo 2
b) Observa que a é a primeira derivada dessa função desenhada ali acima! Ele nos fala que essa segunda derivada tem pelo menos duas soluções reais distintas. Isso significa que ela cruza o eixo x duas vezes. Esses sãos os pontos que representariam os máximos e mínimos da função desenhada acima. Como ela tem um máximo e um mínimo, logo terá duas soluções reais distintas.
Passo 3
c) em
Bom, lembra que é a primeira derivada da função desenhada acima, certo? Ele fala que entre 0 e 2 a é positiva, ou seja, nesse intervalo a função desenhada no enunciado tem que ser crescente! Conferindo lá, ela é sim!! Então tranquilo essa alternativa também.
Passo 4
d) Pode ocorrer de a equação ter exatamente uma solução real.
Observa que a nossa função desenhada acima vem de , ou seja, é crescente a vida toda, logo ela estava certamente acima do eixo x.
Do lado direito da função desenhada ela vai para sempre estando abaixo do eixo x, logo, a será sempre decrescente.
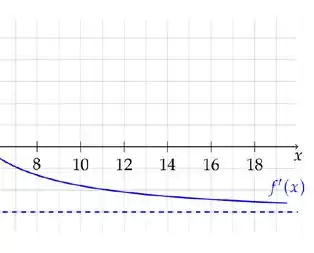
Logo podemos afirmar que em algum momento ela vai cruzar o eixo x, logo ela certamente tem pelo menos uma solução real.
Passo 5
e) tem mínimo global.
Mais uma vez vamos lembrar que é a primeira derivada da função desenhada no enunciado.
Como ela vem decrescendo a vida toda, até seu ponto de mínimo, sabemos que ela vai estar começar então em negativo. Aí a função desenhada chega no ponto de mínimo em , logo esse é o ponto onde cruzaria o eixo x. A função desenhada acima fica crescente até , logo nesse intervalo fica acima do eixo , ou seja, positivo. Depois disso a função desenhada no enunciado só decresce, então ela fica sempre abaixo do eixo x, ou seja, em negativo.
Conslução, ela não vai ter um ponto de min, e sim apenas um de max.
Vai ser algo mais ou menos assim