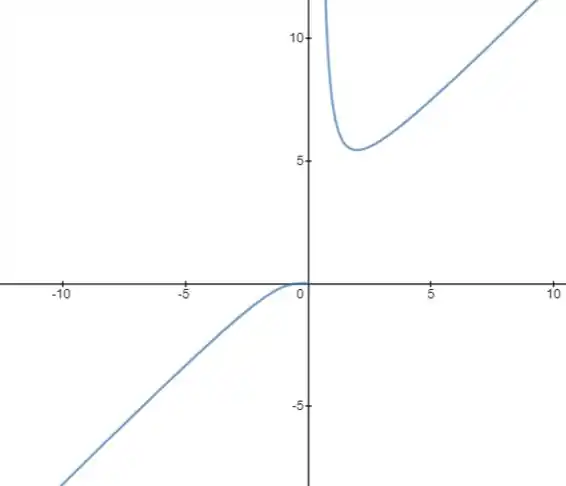
Estude a função dada por
1) Estude o crescimento de , determinando os pontos de máximo e de mínimo locais e globais de , se existirem.
2) Estude a concavidade de
3) Determine as assíntotas do gráfico de , se existirem.
4) Faça um esboço do gráfico de
Passo 1
Primeiro precisamos esturdar os máximos e mínimos, certo? Fazemos isso com a primeira derivada. Bola lá então
Sabemos então que a função pode ser zero em , e sabemos ainda que a função não existe em afinal não adimitos divisão por zero.
Observe que para e maiores que 0, nossa derivada é negativa, logo a função é decrescente
Para valores maiores que 2 a derivada é positiva, logo a é crescente
Temos então que 2 é um valor de mínimo
Vamos analisar
Temos então a função crescente.
Passo 2
Para estudarmos a concavidade, vamos usar a segunda derivada.
Por essa função sabemos apenas que ele não existe em , então vamos analisar esse ponto.
Para
Opa, positivo, então concavidade virada pra cima nesse intervalo.
Para
Negativo, logo, concavidade para baixo.
Temos então uma concavidade para baixo até , depois temos concavidade para cima.
Passo 3
Para determinarmos as assíntotas horizontais, queremos saber como a função se comporta quanto
O mesmo acontece para .
Para as assíntotas verticais, analisamos o comportamento dela quando tende aos valores onde ela não existe. Observaque não admitomos divisão por zero, logo, bora fazer esse limite aí.
Aplicando a regra de L’hospital
Agora
Com isso tudo na mão agora é só montar nossa integral.
Passo 4
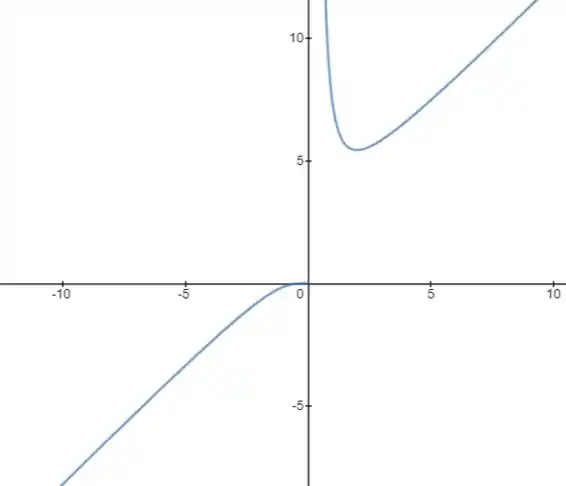
Observa os pontos que precisamos pra montar o gráfico que descobrimos anteriormente nos cálculos.
Resposta