Seja uma função derivável. O gráfico de sua derivada está ilustrado abaixo.
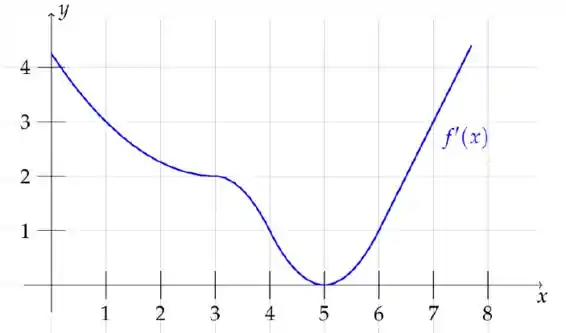
A afirmação que pode não estar correta é:
a)
b)
c)
d)
e)
Passo 1
Lembra do Teorema do valor médio? É isso que a gente vai usar pra sair dessa situação aqui.
Sendo que esse é um ponto existente entre e
Passo 2
Analisando a primeira afirmação temos
Observando o gráfico da derivada, observamos que no intervalo entre 4 e 6, sua derivada varia entre seu valor mínimo que é zero, e o máximo que é um. Logo
Para
Para
Então sabemos que a afirmação é verdadeira.
Agora vamos ter que fazer o mesmo passo a passo pras outras alternativas.
Passo 3
Analisando a primeira afirmação temos
Observando o gráfico da derivada, observamos que no intervalo entre 3 e 6, sua derivada varia entre seu valor mínimo que é zero, e o máximo que é dois. Logo
Para
Para
Então sabemos que a afirmação é falsa, pode ser ainda que esteja entre também, segundo nosso teorema.
Passo 4
Analisando a primeira afirmação temos
Observando o gráfico da derivada, observamos que no intervalo entre 1 e 3, sua derivada varia entre seu valor mínimo que é 2, e o máximo que é 3. Logo
Para
Para
Então sabemos que a afirmação é verdadeira.
Passo 5
Analisando a primeira afirmação temos
Observando o gráfico da derivada, observamos que no intervalo entre 3 e 5, sua derivada varia entre seu valor mínimo que é zero, e o mpaximo que é dois. Logo
Para
Para
Então sabemos que a afirmação é verdadeira.
Passo 6
Analisando a primeira afirmação temos
Observando o gráfico da derivada, observamos que no intervalo entre 4 e 7, sua derivada varia entre seu valor mínimo que é zero, e o máximo que é 3. Logo
Para
Para
Então sabemos que a afirmação é verdadeira.