P2 de Cálculo 1 da USP - 2020
Cálculo 1 - USP
Decida se cada uma das afirmações abaixo é verdadeira ou falsa.
1. Se é derivável com derivada contínua e , para todo Então, o comprimento do gráfico de é, no mínimo,
2. Se são contínuas e então
3. Se é uma função contínua e ímpar então qualquer primitiva de é par.
4. Se é contínua então existe tal que .
Ver solução completaUma partícula desloca-se sobre um eixo com 10 Km de extensão, conforme figura abaixo. Sua velocidade instantânea é dada, em , pode para . No instante , a partícula está à direita da origem .

Pode-se afirmar que:
1. A distância da partícula ao ponto é mínimo no instante
2. A distância da partícula ao ponto é mínimo no instante
3. A distância da partícula ao ponto é mínimo no instante
4. A distância da partícula ao ponto é mínimo no instante
5. A partícula está sempre à direita de
Ver solução completaUma tela de cinema de de altura está fixado numa parede, com sua base 4 m acima de seus olhos conforme a figura abaixo.
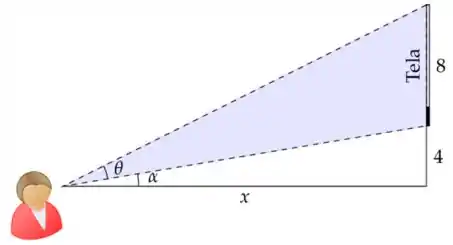
Se é a distância a que você deve ficar da parede para que seu ângulo de visão da tela seja máximo, então vale:
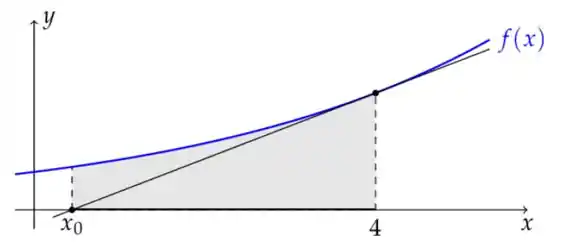
Ver solução completaConsidere dada por , e a reta tangente a seu gráfico no ponto de abscissa 4. Se é interceptado desta reta com o eixo , então a área hachurada na figura (fora de escala) abaixo é: