Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 681234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666769707172737475767778798081828384858687888990919293949596979899100

Enunciado

O volume do sólido obtido pela rotação em torno do eixo O x , da região

A = x , y ∈ R : 0 ≤ x ≤ π   e t g x 2 ≤ y ≤ s e n x , indicado na figura abaixo é:

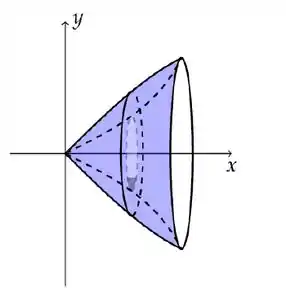
Passo 1

Para esse caso podemos aplicar uma formulinha diretona, onde

V = ∫ a b π f x 2 - g x 2   d x

Onde a f ( x ) é a função que passa por fora e g ( x ) a mais interna. Assim temos

V = ∫ 0 π π s e n 2 x - t g 2 x 4   d x

Passo 2

Agora vai ser só reolvermos essa belezinha. Começamos tirando π de dentro da integral

V = π ∫ 0 π s e n 2 x - t g 2 x 4   d x

V = π ∫ s e n 2 x d x - 1 4 ∫ t g 2 x   d x

Resolvendo primeiramente integral do seno

∫ s e n 2 x d x = ∫ 1 2 - 1 2 cos ⁡ 2 x   d x

= - 1 2 c o s ∫ cos ⁡ 2 x d x + 1 2 ∫ d x

2 x = u → d u = 2 d x → d x = d u 2

= x 2 - 1 4 ∫ cos ⁡ u d u

= x 2 - s e n u 4

= x 2 - s e n 2 x 4

= x - s e n x cos ⁡ x 2

Passo 3

Temos ainda que resolver a parte da integral referenta á tangente.

∫ t g 2 x   d x

= ∫ sec 2 ⁡ x - 1 d x

= t g x - x

Essa foi tranquilinha, haha.

Passo 4

Agora é sol voltar com os resultados que encontramos e aplicar o intervalo de integração

V = π ∫ s e n 2 x d x - 1 4 ∫ t g 2 x   d x

V = π x - s e n x cos ⁡ x 2 - 1 4 t g x - x 0 π

V = π π - s e n π cos ⁡ π 2 - 1 4 t g π - π 0 π

V = π 2 2 + π 2 4 = 3 π 2 4

Passo 5

Resposta

3 π 2 4

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .