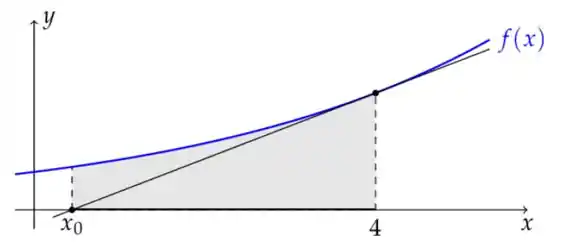
Considere dada por , e a reta tangente a seu gráfico no ponto de abscissa 4. Se é interceptado desta reta com o eixo , então a área hachurada na figura (fora de escala) abaixo é:
Passo 1
Primeiro passo pra gente aqui vai ser descobrir qual a equação dessa reta tange aí, afinal, com isso, a gente descobre o , percebe?
Bora lá então
Primeiro passo é encontar um ponto na nossa função
Segundo encontramos o
E por último escrevemos nossa equação na forma
Lesgô então
Passo 2
Encontrando um ponto conhecido na nodda . Pelo esboço, somos induzidos a usar o 4, certo? Bora lá então
Perfeito, nosso segundo passo agora é encontrar
Por último então montamos
Passo 3
Bom, isso aí em cima é nossa equação da reta já! Não precisa sair mexendo em nada pra arrumar!! Quanto menos trabalho melhor hahaha
Observa que o ponto que estamos procurando é o , que está contido na reta tangente, e passa pelo
Então vamos só substituiro o na equação da nossa reta tangente.
Passo 4
Agora vamos precisar encontrar a área abaixo da função entre os pontos 1 e 4. E isso é o que? Parabéns se você respondeu a integral definida entre 1 e 4, haha.