Uma tela de cinema de de altura está fixado numa parede, com sua base 4 m acima de seus olhos conforme a figura abaixo.
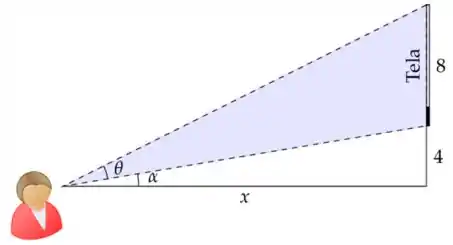
Se é a distância a que você deve ficar da parede para que seu ângulo de visão da tela seja máximo, então vale:
Passo 1
Para resolvermos essa questão, devemos lembrar do conceito de derivada implícita e ponto máximo de uma função crescente.
Observando a imagem vemos que temos um ângulo , relativo á altura de seus olhos até a base da tela, relativo à altura de seus olhos ao quadro, e podemos chamar de a soma desses dois ângulos.
Buscamos a distância entre o observador e a parede tal que o ângulo seja () seja máximo.
Passo 2
Observe que podemos ultilizar a fórmula de soma de arcos para expressarmos a relação entre a distancia e as alturas.
Observe que o triângulo formado pela visão do observador e as alturas é um triângulo retângulo, logo vale dizer que
Passo 3
Somando os valores e substituindo teremos
Isolando a
Passo 4
Próximo passo é calcularmos a derivada, afinal estamos trabalhando com otimozação,c erto...
Devemos fazê-lo de forma que seu seja nulo, afinal a função cresce até seu ponto de máximo! (derivada igual a zero). Assim
Passo 5
Bom, mas a questão não para ainda por aí. Temos o valor de , mas queremos , certo?
Lembra que
Sabemos então que vale
Temos ainda que
Sabemos então que vale . Então:
Passo 6
Bom, mas a relação que queremos é , logo