Lista Continuidade - UTFPR de Cálculo Diferencial e Integral 1 da UTFPR - 2022.2

11 – Considere a função

a) Existe uma constante para qual a constante seja contínua em ? Justifique sua resposta.

b) se existir uma constante tal que seja contínua em , esboce o gráfico de .

Determine se as seguintes funções são contínuas em :

Determine se as seguintes funções são contínuas em :

Para cada afirmação, assinale V se ela for verdadeira, ou F se ela for falsa

( ) Toda função polinomial é contínua em

( ) Se for contínua em , então

( ) Para uma função , se , então é contínua em toda parte

( ) Toda função racional possui descontinuidade onde o denominador é zero

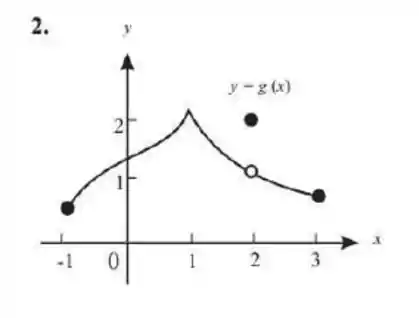
Observando o gráfico de na figura abaixo, determine se a função é contínua ou descontínua em cada um dos seguintes valores de

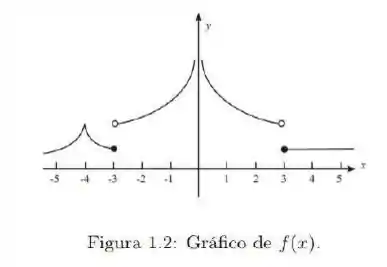
1. x = - 1

Determine se as seguintes funções são contínuas em :

Para cada gráfico da figura , determine se a função traçada é contínua no intervalo . Se não for contínua, aponte onde ela deixa de ser contínua e diga qual o tipo de descontinuidade em questão.

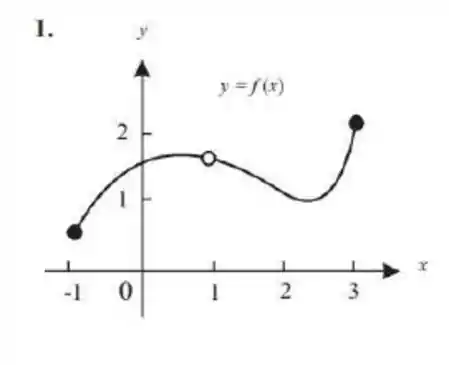
Considere a função

Responda:

1. Existe ?
2. Existe ?
3. ?
4. é contínua em ?
5. Existe ?
6. Existe ?
7. ?
8. é contínua em ?

1.3 , determine se a função traçada é contínua no intervalo . Se não for contínua, aponte onde ela deixa de ser contínua e diga qual o tipo de descontinuidade em questão.

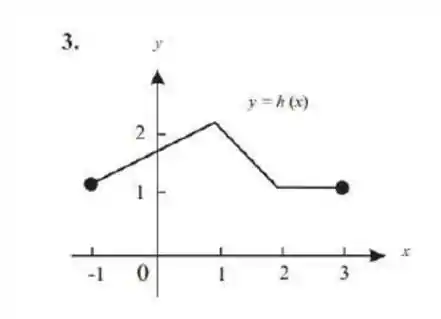
Para cada gráfico da figura , determine se a função traçada é contínua no intervalo . Se não for contínua, aponte onde ela deixa de ser contínua e diga qual o tipo de descontinuidade em questão.

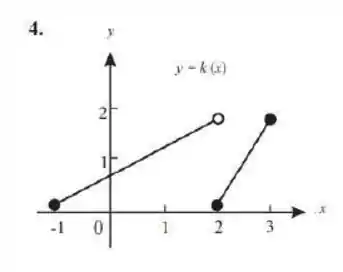
Para cada gráfico da figura , determine se a função traçada é contínua no intervalo . Se não for contínua, aponte onde ela deixa de ser contínua e diga qual o tipo de descontinuidade em questão.

Determine um valor para a constante , se possível, que torna a função

contínua

Determine, se existirem, os valores de para os quais cada uma das seguintes funções é descontínua

7 – Determine, se existirem, os valores de para os quais cada uma das seguintes funções é descontínua:

c)

7 – Determine, se existirem, os valores de para os quais cada uma das seguintes funções é descontínua:

d)

7 – Determine, se existirem, os valores de para os quais cada uma das seguintes funções é descontínua:

b)