UTFPR. Cálculo Diferencial e Integral 1. Lista Continuidade. 2022.2. Questão 7d.
7 – Determine, se existirem, os valores de para os quais cada uma das seguintes funções é descontínua:
d)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Esse é um problema de continuidade em que temos que descobrir em quais pontos de a função é descontínua.
No caso, a função é definida por partes onde quando é diferente de a função assume o comportamento de mas quando é igual a a função é constante e igual a .
Consegue imaginar algum ponto em que a função é descontínua?? 🤔🤔
Uma função de uma variável é contínua quando seus limites laterais são iguais e igual ao valor que a função assume no ponto em questão.
Em outras palavras, uma função é continua quando ela não possui buracos ou escadas na sua imagem.
Entendeu? Vamos analisar essa função então. 😁
Passo 2
Como vemos no passo anterior, os limites laterais da função devem ser iguais e tender à imagem de no ponto.
No caso, a suspeita é o ponto já que é o ponto em que a função muda de comportamento.
Ou seja, se a função é contínua, então
O limite de quando tende a pela esquerda deve ser igual a , que é o valor que a função assume em e que deve ter igual ao limite de quando tende a pela direita.
Aproximando pela esquerda, assumimos valores infinitesimalmente menores que , ou seja , e .
Perceba que quanto mais próximo fica de pela esquerda, menor é o valor da função. Ou seja, para valores infinitesimais menores que , a função tende a valores tão grandes em módulo, mas com sinais negativos que podemos dizer que tende a
Logo o limite de para é igual a
Entendeu essa parte? 👀
Passo 3
Agora vamos calcular o limite de quando tende a pela direita, ou seja, para valores infinitesimalmente maiores que .
Vamos analisar a imagem da função para , e .
Quase da mesma forma que na outra aproximação, aproximando a pela direita, a função assume valores muito grandes e positivos e quanto mais próximo de , maior é a imagem.
Portanto, podemos dizer que o limite de para é igual a
Dessa forma, vemos que os três resultados foram divergentes
O que não é possível, logo a função é descontínua em .
Para matar a curiosidade, podemos observar o gráfico da função.
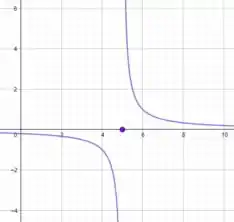
Viu só? A descontinuidade nesse caso é muuuito grande...
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
é descontinua em .