Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Continuidade

Ver Teoria
Exercício 240123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UTFPR– Cálculo 1 – Lista de Continuidade – Questão 5.3

1.3 , determine se a função traçada é contínua no intervalo - 1,3 . Se não for contínua, aponte onde ela deixa de ser contínua e diga qual o tipo de descontinuidade em questão.

Passo 1

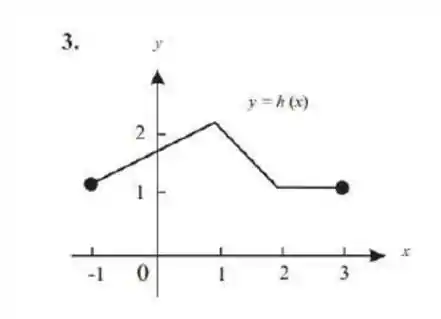
Olá pessoal, tudo bem? O problema deu o gráfico de uma função definida em [ - 1,3 ]

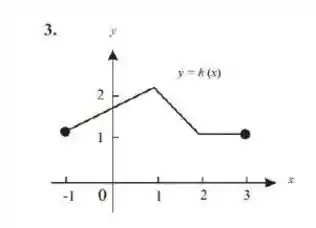
E perguntou se ela é contínua nesse intervalo. Você lembra de os critérios para uma função ser contínua?

São esses três:

  1. Os limites laterais devem existir (não ser ∞ ) e serem iguais lim x → a + ⁡ f ( x ) = lim x → a - ⁡ f ( x )
  2. Deve existir a função aplicada no ponto f ( a )
  3. E os resultados de ( 1 ) e ( 2 ) devem ser iguais!

E não só isso: pediu também para que caso haja uma descontinuidade, a gente classifique! Você lembra quais são os casos que existem de descontinuidade?

Temos também três tipos de descontinuidade:

  • Descontinuidade removível: é quando existe o limite (ou seja, os limites laterais existem e são iguais entre si), mas a função no ponto assume outro valor

    • lim x → x 0 + ⁡ f ( x ) = lim x → x 0 - ⁡ f ( x ) ≠ f ( x 0 )

  • Descontinuidade de salto (ou de 1ª espécie): quando os limites laterais são finitos mas diferentes entre si. Dizemos que ali não há limite.

    • lim x → x 0 + ⁡ f ( x ) ≠ lim x → x 0 - ⁡ f ( x )

  • Descontinuidade infinita (ou de 2ª espécie): quando os limites laterais (um ou os dois) resultam em ± ∞ . Nesse caso também não existe o limite.

lim x → x 0 + ⁡ f ( x ) = ± ∞     e \ o u   lim x → x 0 - ⁡ f ( x ) = ± ∞

Tranquilo?

Outra forma de enxergarmos uma descontinuidade é imaginar que estamos desenhando o gráfico no papel com um lápis. Se para desenhar for preciso tirar o lápis do papel, então nesse ponto é bem provável que haja uma descontinuidade! Ok?

Então a ideia é usar esse conceito de continuidade e seus tipos para analisar o gráfico!

Mas pode ficar tranquilo, vou fazer passo a passo com você! Bora começar?

Passo 2

Vamos retomar nosso gráfico:

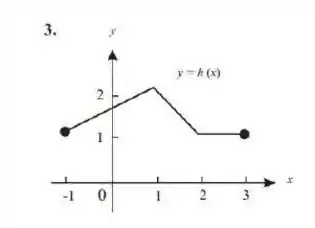
Colocando nosso lápis imaginário em x = - 1 e desenhando por cima da função, não precisamos tirar em nenhum momento da folha!

x = 1 , a função está toda definida no intervalo e, portanto, é contínua em [ - 1,3 ]

Você pode confundir com diferenciabilidade! No bico, a função pode ser contínua, mas ela não é diferenciável, mas isso é papo para outro momento!

Por enquanto está tudo bem, essa função é contínua! Beleza? Bora praticar mais?

Resposta

n ã o   e x i s t e

Exercícios de Livros Relacionados

Explique por que a função é descontínua no dado número a . Esboce o gráfico da função. f x = x 2 - x x 2 - 1 , x ≠ 1 1 , x = 1 ,a = 1
Localize as descontinuidades da função e ilustre com um gráfico. y = ln ⁡ t g 2 x
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. R x = x 2 + 2 x - 1
Use a definição de continuidade e propriedades dos limites para demonstrar que a função é contínua em um dado número a . f x = x 2 + 7 - x , em a = 4 .
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. F x = s e n - 1 ( x 2 - 1 )