UTFPR. Cálculo Diferencial e Integral 1. Lista Continuidade. 2022.2. Questão 11.
11 – Considere a função
a) Existe uma constante para qual a constante seja contínua em ? Justifique sua resposta.
b) se existir uma constante tal que seja contínua em , esboce o gráfico de .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão, temos uma função que é definida por partes, quando , assume e quando , assume .
A ideia no item a) é obter um valor de de modo que a função seja contínua em .
Já no item b), após obter o valor do item a), esboçar o gráfico de .
Tem ideia de como fazer isso? 🤔
Quando , assume a função e repentinamente quando , assume a função .
Para ser continua em , essa mudança de comportamento deve ser tão suave que o valor de em deve ser igual a em .
Veja só como vamos fazer isso! 😁
Passo 2
Em a função assume qual valor?
Nesse ponto assume , correto? Ou seja, se , então
Nesse caso quando estiver infinitesimalmente maior que , deve ser também infinitesimalmente igual a .
Dessa forma, o limite de de quando tende a pela direita, deve ser igual a
E quando tende a pela direita assume , entendeu?
Ou seja, o que temos que calcular é
E forçar esse resultado ser igual a
Portanto temos que dizer que
Se substituirmos por , vamos obter
Como é uma constante então temos que
O que é impossível! Portanto não existe um valor para que faça ser contínua em !
Tranquilo até aqui? 🤔
Passo 3
Já no item b), temos que esboçar o gráfico de após definir .
Mas acabamos de obter que não existe, então como para tende ao infinito e para tende a em . A função não é contínua.
Se esboçarmos o gráfico de , vamos obter algo parecido com isso
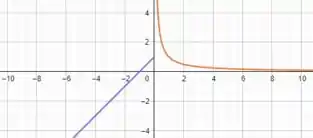
Nesse caso, usamos e se usarmos qualquer valor para , o resultado será o mesmo!
tende ao infinito em .
É isso!
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
não existe!