UTFPR– Cálculo 1 – Lista de Continuidade – Questão 1
Para cada afirmação, assinale V se ela for verdadeira, ou F se ela for falsa
( ) Toda função polinomial é contínua em
( ) Se for contínua em , então
( ) Para uma função , se , então é contínua em toda parte
( ) Toda função racional possui descontinuidade onde o denominador é zero
Passo 1
E aí, tudo bem? Essa questão é de julgar se as sentenças são verdadeiras ou falsas, então precisamos analisar uma a uma
Mas antes, vamos relembrar quais são as condições para que uma função seja contínua em um determinado ponto?
Para que uma função seja considerada contínua em um ponto , deve acontecer três coisas
- Os limites laterais devem existir e serem iguais
- Deve existir a função aplicada no ponto
- E os resultados de e devem ser iguais!
Então a ideia é analisar afirmativa por afirmativa, lembrando das condições para uma função ser contínua e verificar se são verdadeiras ou falsas
Mas relaxa, vou fazer passo a passo com você!
Passo 2
( ) Toda função polinomial é contínua em
Uma função polinomial é uma função do tipo
E ela não apresenta nenhum ponto que mereça nossa atenção, já que seu domínio são todos os reais! Não tem como resultar em uma indeterminação!
Isso significa que um polinômio é sim contínuo em todo conjunto dos !
Sendo assim a afirmativa é verdadeira!
Tudo bem até aqui?
Passo 3
( ) Se for contínua em , então
Lembra o que falei sobre continuidade? Vamos resgatar as condições:
- Os limites laterais devem existir e serem iguais
- Deve existir a função aplicada no ponto
- E os resultados de e devem ser iguais!
A primeira condição fala sobre os limites laterais. Se eles existem e são iguais, isso significa que o limite existe nesse ponto
E o valor do limite é o valor dos limites laterais (que são iguais, certo?)
E mais que isso, se a função é contínua, o limite no ponto é igual ao valor da função no ponto! Então, se a função é contínua em , então
E isso significa que essa segunda afirmativa é verdadeira também!
Passo 4
( ) Para uma função , se , então é contínua em toda parte
Essa afirmativa diz que se não tivermos pontos “ruins” no domínio, ou seja, a função é bem-comportada em todos os pontos, então ela é contínua em toda parte. Será?
Não! Embora uma função seja bem-comportada, em um determinado ponto a função pode “saltar”, assim:
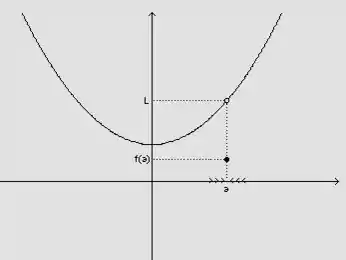
A função existe em todos os pontos, mas em um determinado
E portanto, ali a função não é contínua!
Então essa afirmativa é falsa
Partiu analisar a última?
Passo 5
( ) Toda função racional possui descontinuidade onde o denominador é zero
Você lembra o que acontece quando dividimos por zero? Por exemplo
Quando calculamos esse tipo de limite, sabemos que se aproxima de , mas por valores maiores do que . Sabemos que
Pois é pouca coisa maior do que , mas é maior! Então no nosso limite dividimos por um número positivo e bem (beeeem) pequeno! O resultado disso é
E isso simboliza uma descontinuidade! Então descontinuidade em funções racionais é justamente isso, é onde o denominador é zero!
Portanto essa última afirmativa também é verdadeira!
Vamos recapitular os resultados:
(V) Toda função polinomial é contínua em
(V) Se for contínua em , então
(F) Para uma função , se , então é contínua em toda parte
(V) Toda função racional possui descontinuidade onde o denominador é zero
Beleza? É isso! Espero ter ajudado!