UTFPR. Cálculo Diferencial e Integral 1. Lista Continuidade. 2022.2. Questão 7c.
7 – Determine, se existirem, os valores de para os quais cada uma das seguintes funções é descontínua:
c)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão, temos uma função que é definida por partes em que quando , a função se comporta como a função , já quando a função é constante e igual a .
Dessa forma, temos que obter os pontos em que a função é descontínua, se existirem.
Tem ideia de como vamos obter isso? 🤔🤔
Dizemos que uma função de uma variável é descontínua quando os limites laterais da função em um ponto divergem entre si ou do valor que a função assume.
Em outras palavras, uma função bidimensional é continua se não tiver buracos ou degraus em sua imagem!
E aí, acha que essa função é contínua? 😁
Bora ver!
Passo 2
nessa função, a mudança de comportamento acontece em já que em pontos diferentes tem o mesmo comportamento, então nossa principal suspeita é nesse ponto.
Em a função assume a imagem , então se for continua nesse ponto, os limites laterais de devem ser iguais a . Ou seja
Para o limite de nos aproximando de pela esquerda, ou seja, para valores infinitesimalmente menores que , temos
Perceba que quanto mais nos aproximamos de , menor o valor da função
Por exemplo, em , e temos
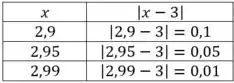
Dessa forma, se aproxima de , logo o limite de se aproximando de pela esquerda, é igual a
Tranquilo até aqui? 👀
Passo 3
Agora vamos fazer o mesmo só que nos aproximando pela direita, ou seja, por valores infinitesimalmente maiores que .
Agora fazemos para , e , cada vez nos aproximando mais de
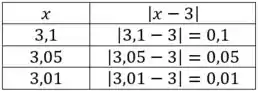
Perceba que quanto mais nos aproximando de nesse caso, mais próximo de nossa função assume.
Logo, o limite de quando tende a pela direita é igual a também
Juntando os resultados que obtemos, vemos que
A função é descontínua em já que nesse ponto, a função vale mas nos seus arredores a função tende a .
Vamos dar uma olhada no gráfico que essa função forma.
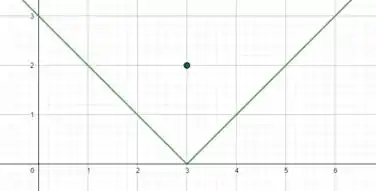
Viu só?
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
é descontínua em .