UTFPR– Cálculo 1 – Lista de Continuidade – Questão 3
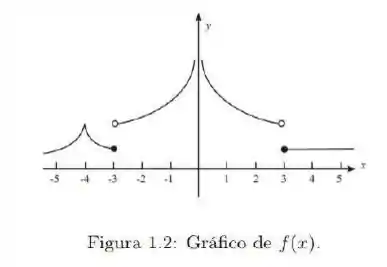
Observando o gráfico de na figura abaixo, determine se a função é contínua ou descontínua em cada um dos seguintes valores de
-
x = - 1
Passo 1
E aí, tudo bem? Essa questão nos dá o gráfico de uma função e pergunta se ela é contínua em vários pontos de seu domínio
Mas você lembra de as condições para uma função ser contínua em um ponto?
São essas três:
- Os limites laterais devem existir (não ser ) e serem iguais
- Deve existir a função aplicada no ponto
-
( 1 ) e devem ser iguais!
Então a ideia é analisar ponto a ponto o gráfico, e verificar se os limites são iguais entre si e iguais à função no ponto (bolinha fechada)
Outra maneira de ver é: para desenhar a função em torno desse ponto, você tira o lápis do papel? Se a resposta for sim, então ali temos uma descontinuidade! Se não, então ela é contínua em torno!
Mas pode ficar tranquilo, vou fazer passo a passo com você!
Passo 2
- Em torno de :
-
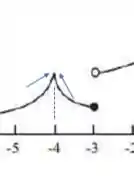
x = - 4 - Em torno de :
-
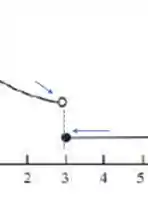
x = 3 : - Em torno de :
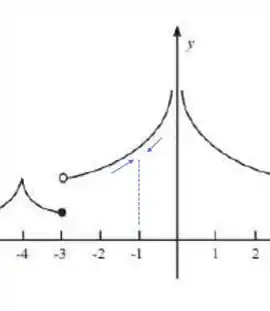a função é contínua, bem tranquilo!
Tudo bem até aqui?
Passo 3
Embora apresente um bico (ponto em que não temos uma reta tangente e portanto não é diferenciável), a função tende ao mesmo ponto pelos dois lados.
E você não precisa tirar o lápis do papel para desenhar esse bico, então a função é mesmo contínua ali!
Passo 4
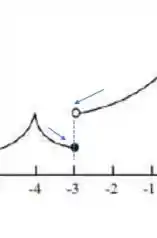
Percebeu que em torno desse ponto as setinhas se desencontram? Isso significa que os limites laterais são diferentes! Portanto ali nossa função não é contínua
(para desenhar a função vamos precisar tirar do papel não é verdade? Essa maneira de ver sempre funciona mas é menos formal)
Passo 5
Vamos que aqui as setas também se desencontram! Os limites laterais são diferentes, e isso nos mostra que em há novamente uma descontinuidade!
Partiu avaliar o último ponto?
Passo 6
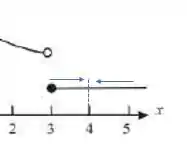
vamos recapitular as respostas?
E é isso! Espero ter ajudado! Vamos para a próxima?