Listas GMA de Cálculo IA da UFF - Lista 15

Esboce o gráfico de:

Esboce o gráfico da função e dê explicitamente o que se pede:

• Domínio de
• Paridade de
• Equações das assíntotas verticais e horizontais do gráfico
• Intervalos de em que é contínua
• Pontos de em que a tangente ao gráfico é vertical
• Intervalos de onde é crescente e onde é decrescente
• Extremos relativos de e os respectivos pontos de onde ocorrem
• Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
• Extremos absolutos de e os respectivos pontos de onde ocorrem;
• Imagem de

Esboce o gráfico da função e dê explicitamente o que se pede:

• Domínio de
• Paridade de
• Equações das assíntotas verticais e horizontais do gráfico
• Intervalos de em que é contínua
• Pontos de em que a tangente ao gráfico é vertical
• Intervalos de onde é crescente e onde é decrescente
• Extremos relativos de e os respectivos pontos de onde ocorrem
• Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
• Extremos absolutos de e os respectivos pontos de onde ocorrem;
• Imagem de

Esboce o gráfico da função e dê explicitamente o que se pede:

• Domínio de
• Paridade de
• Equações das assíntotas verticais e horizontais do gráfico
• Intervalos de em que é contínua
• Pontos de em que a tangente ao gráfico é vertical
• Intervalos de onde é crescente e onde é decrescente
• Extremos relativos de e os respectivos pontos de onde ocorrem
• Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
• Extremos absolutos de e os respectivos pontos de onde ocorrem;
• Imagem de

Esboce o gráfico da função e dê explicitamente o que se pede:

• Domínio de
• Paridade de
• Equações das assíntotas verticais e horizontais do gráfico
• Intervalos de em que é contínua
• Pontos de em que a tangente ao gráfico é vertical
• Intervalos de onde é crescente e onde é decrescente
• Extremos relativos de e os respectivos pontos de onde ocorrem
• Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
• Extremos absolutos de e os respectivos pontos de onde ocorrem;
• Imagem de

Esboce o gráfico da função e dê explicitamente o que se pede:

• Domínio de
• Paridade de
• Equações das assíntotas verticais e horizontais do gráfico
• Intervalos de em que é contínua
• Pontos de em que a tangente ao gráfico é vertical
• Intervalos de onde é crescente e onde é decrescente
• Extremos relativos de e os respectivos pontos de onde ocorrem
• Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
• Extremos absolutos de e os respectivos pontos de onde ocorrem;
• Imagem de

Esboce o gráfico da função e dê explicitamente o que se pede:

• Domínio de
• Paridade de
• Equações das assíntotas verticais e horizontais do gráfico
• Intervalos de em que é contínua
• Pontos de em que a tangente ao gráfico é vertical
• Intervalos de onde é crescente e onde é decrescente
• Extremos relativos de e os respectivos pontos de onde ocorrem
• Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
• Extremos absolutos de e os respectivos pontos de onde ocorrem;
• Imagem de

Esboce o gráfico da função e dê explicitamente o que se pede:

• Domínio de
• Paridade de
• Equações das assíntotas verticais e horizontais do gráfico
• Intervalos de em que é contínua
• Pontos de em que a tangente ao gráfico é vertical
• Intervalos de onde é crescente e onde é decrescente
• Extremos relativos de e os respectivos pontos de onde ocorrem
• Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
• Extremos absolutos de e os respectivos pontos de onde ocorrem;
• Imagem de

Esboce o gráfico de

Seja duas vezes diferenciável e tal que

• , e

•, , ,

• se e se

• o gráfico de está dado abaixo

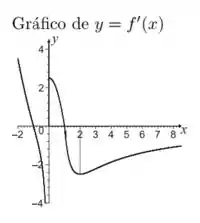
Nestas condições,

(a) prove que

(b) prove que

(c) esboce um possível gráfico de

Esboce o gráfico de

Esboce o gráfico da função e dê explicitamente o que se pede:

• Domínio de
• Paridade de
• Equações das assíntotas verticais e horizontais do gráfico
• Intervalos de em que é contínua
• Pontos de em que a tangente ao gráfico é vertical
• Intervalos de onde é crescente e onde é decrescente
• Extremos relativos de e os respectivos pontos de onde ocorrem
• Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
• Extremos absolutos de e os respectivos pontos de onde ocorrem;
• Imagem de

Esboce o gráfico de

Esboce o gráfico de

Esboce o gráfico de

Esboce o gráfico de