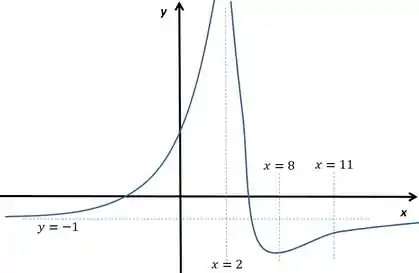
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Passo 1
- A gente sabe que denominador não pode ser zero, correto? Então a função ali não pode assumir , caso contrário vai dar problema. De resto, nenhum problema quanto à existência da função. Assim,
- A função do numerador até é par em relação ao eixo , porém a de baixo não tem nenhuma simetria. Essa divisão, portanto, necessariamente vai gerar uma função sem paridade nenhuma.
Passo 2
- As assíntotas verticais estão relacionadas aos pontos onde o domínio não está definido. Usando o
As assíntotas horizontais, por outro lado, tem a ver com a tendência do limite de no infinito. Usando os limites para , achamos o seguinte:
Para o limite será o mesmo! Assim, temos que é uma assíntota horizontal.
Passo 3
- A continuidade da função depende do domínio dela. Onde não existirem descontinuidades no domínio ela será contínua.
Assim, é contínua em .
- Os pontos onde a tangente ao gráfico é vertical seriam aqueles pontos onde a função apresenta um crescimento ou decrescimento infinito, ou seja, nas assíntotas verticais.
Para essa , isso só acontece em .
Passo 4
- Para definir se a função é crescente ou decrescente, devemos olhar para o sinal de sua derivada: onde ela é positiva, cresce; onde é negativa, decresce. Vamos calcular a derivada:
A gente conclui que o sinal depende só de e de . Confere aqui no quadrinho então:
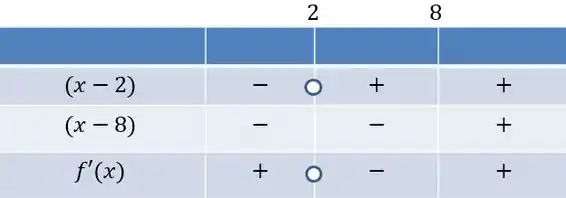
Logo, cresce de até e a partir de . Entre e decresce.
- Os extremos relativos acontecem onde .
Temos que apenas satisfaz isso. Nesse ponto, vai valer:
No caso, como a derivada é negativa antes e positiva depois esse é um ponto de mínimo relativo.
Passo 5
- Definimos a concavidade de acordo com o sinal da derivada segunda: se for positiva, concavidade para cima; se negativa, para baixo. Vamos calcular a derivada segunda então!
Sabemos que o denominador tá elevado a uma potência par, o que faz dele sempre positivo. Então o nosso sinal só depende do termo de cima, correto? Assim, a concavidade é para cima quando , pois vamos estar dividindo positivo por positivo, dando positivo e para baixo em , pois vamos estar dividindo negativo por positivo, dando negativo.
E como o ponto de inflexão é o ponto exato em que a concavidade muda de sinal, igualando a segunda derivada à temos:
Nosso ponto de inflexão é então .
- Para pensar em extremos relativos temos que analisar se os limites da função para são maiores ou menores que os pontos críticos (onde ).
No caso, e e no resto do domínio nenhum outro ponto tem um valor menor, concluímos que é ponto de mínimo absoluto.
- A imagem de consiste em todos os valores que ela pode assumir.
Como seu menor valor é e em a função tende para , sua imagem é:
Passo 6
- Agora juntamos todas as informações para desenhar o nosso gráfico.