Esboce o gráfico de:
Passo 1
Essa é uma função que pode assustar à primeira vista, mas vamos dissecá-la com cuidado.
Primeiramente, podemos ver que ela não tem nenhum tipo de restrição, seja quociente, raiz quadrada ou logaritmo, então o seu domínio é todo o .
Passo 2
A imagem dessa função dá pra achar tranquilamente também!
é uma constante positiva, então elevando ela a qualquer valor (seja positivo ou negativo) vamos obter um número positivo. Ou seja:
Passo 3
Agora vamos caçar assíntotas!
Como o domínio de é todo o , ela não tem assíntota vertical. Mas podemos procurar assíntotas horizontais, calculando os limites no infinito:
Opa, então é uma assíntota horizontal da função!
Passo 4
Agora vamos ver como é o crescimento da , analisando o sinal da sua primeira derivada.
Pela regra da cadeia:
Repare que:
Ou seja, temos:
Ou seja, a função é sempre crescente, ela só dá uma pausinha ali no mas não chega a decrescer em momento algum.
Passo 5
Só nos resta descobrir a concavidade da função. Derivando de novo:
Temos
Logo,
Passo 6
Vejamos o sinal disso aí…. Temos que:
Agora vamos ver quando o outro termo se anula:
Então ou , ou:
A função tem 2 pontos de inflexão: e .
Passo 7
Temos que
Da mesma forma:
E entre os 2 pontos de inflexão, a derivada segunda é negativa.
Resumindo:
Ou seja, tem concavidade para cima em e concavidade para baixo em .
Passo 8
Com isso tudo já dá pra esboçar o gráfico!!
Hm na verdade falta só mais uma coisinha....que você talvez já tenha se perguntado: quanto diabos vale ?? Temos que usar o valor dele no gráfico né!
Vamos dar uma estimada nesse rapaz sem calculadora. Isso é um treino pra vida!
Primeiramente: quanto vale mais ou menos ?
Olha, sabemos que e , sendo que .
A função logaritmo natural cresce devagariiinho, então podemos chutar:
Passo 9
E agora temos que tirar a raiz cúbica disso:
Vejamos, o quê ao cubo dá 5? 1 ao cubo dá 1, e 2 ao cubo dá 8, então
Vamos testar :
Ainda está muito baixo. Um valor interessante de testar é :
Ok, então digamos que .
E digamos que , já que , só pegamos um número um pouco maior que .
Passo 10
Disso tudo tiramos que:
Podemos usar esse valor pro esboço!
Obs.: um valor mais preciso, achado com a calculadora, é . Viu que só com estimações relativamente simples dá pra chegar perto do resultado? ;)
Passo 11
Resumindo o gráfico:
- Ele vem lá de , onde está bem próximo zero, e com concavidade para cima, crescendo devagar.
- Mais ou menos em ele passa a ter concavidade para baixo.
- Ele chega na horizontal em , onde vale , e aí muda de novo da concavidade.
- Depois disso ele cresce abruptamente pro infinito.
Lá vai:
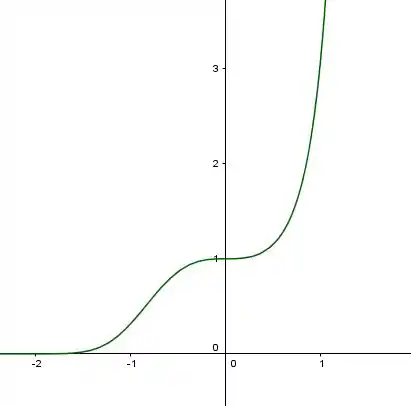
Resposta
(gráfico acima)