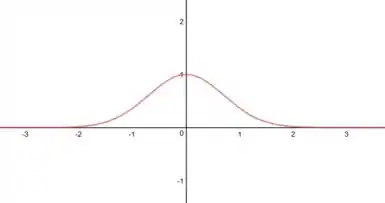
Esboce o gráfico de
Passo 1
Para começar, vamos determinar o domínio da função. Ela pode ser reescrita da seguinte maneira
A única restrição seria quando , mas como isso nunca ocorre não há restrições para o domínio, ou seja, ele é todo o conjunto dos reais.
Passo 2
Agora, vamos ver se a função tem alguma paridade, ou seja, se ela é uma função par ou uma função ímpar.
- ?
Sim. Exemplo: . Isso ocorre para todos os pontos do domínio. Ser par significa que a função é simétrica em relação ao eixo . Tudo que ocorre quando ocorre quando .
-?
Não.
Passo 3
Hora de determinar se a função tem assíntotas. Vamos começar pelas verticais. Já que nossa função não tem pontos de descontinuidade, pois o domínio é todo o conjunto dos reais, ela necessariamente não possui assíntotas verticais.
Agora vamos ver as assíntotas horizontais.
Então é assíntota horizontal.
Passo 4
Temos que fazer o estudo do crescimento da função. Vamos derivar e ver onde a derivada é positiva e negativa.
Como o sinal da derivada só será afetado por
- Quando :
- Quando :
A função é crescente quando e decrecente quando .
Passo 5
Agora vamos determinar os máximos e mínimos da função, se existirem. Primeiro temos que achar os pontos críticos.
Achamos como ponto crítico. Como vimos no passo anterior, a derivada passe de positiva pra negativa nesse ponto, logo ele é um máximo da função. Nesse caso é um máximo global, pois não há outros pontos de máximo, visto que não temos fronteira no domínio que poderiam configurar máximos globais. O valor máximo da função é
Passo 6
Estamos quase terminando. Falta estudar a concavidade da função. Para isso, temos que fazer a segunda derivada.
Agora estudamos o sinal.
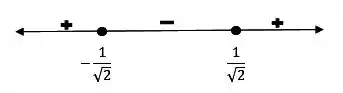
Então quando e , logo ela é côncava para cima nesses intervalos. Quando , , logo a concavidade é para baixo.
Os pontos são pontos de inflexão.
Passo 7
Pronto! Agora podemos juntar tudo que descobrimos e fazer o esboço do gráfico, que fica assim:
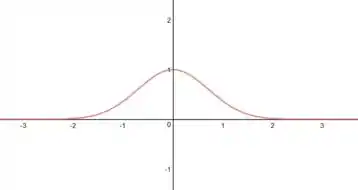
Resposta