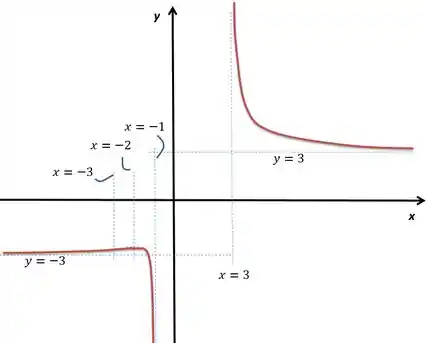
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Passo 1
- A gente sabe que denominador não pode ser zero e não existe raiz de número negativo, correto? Assim, temos que . Por ser uma parábola com a boca para cima, sabemos que ela só será negativa entre as raízes, onde temos ainda
Logo, o domínio será esse:
- Não existe nenhum tipo de simetria ou paridade dessa função.
Passo 2
- As assíntotas verticais estão relacionadas aos pontos onde o domínio tem uma descontinuidade. Usando o limite lateralem e
As assíntotas horizontais, por outro lado, tem a ver com a tendência do limite de no infinito. Usando os limites para , achamos o seguinte:
Assim, temos que e são assíntotas horizontais.
Passo 3
- A continuidade da função depende do domínio dela. Onde não existirem descontinuidades no domínio ela será contínua.
Assim, é contínua em .
- Os pontos onde a tangente ao gráfico é vertical seriam aqueles pontos onde a função apresenta um crescimento ou decrescimento infinito, ou seja, nas assíntotas verticais.
Para essa , isso só acontece em e .
Passo 4
- Para definir se a função é crescente ou decrescente, devemos olhar para o sinal de sua derivada: onde ela é positiva, cresce; onde é negativa, decresce. Então pra nossa função:
Vamos calcular a derivada. E como temos termos com em cima e em baixo, bora usar uma regra do quociente:
Ufa, demorou mas tai, a primeira derivada vai ser:
Se analisarmos bem o denominador, vamos ver que não tem como ele ser nunca negativo. Afinal, essa primeira derivada pode ser reescrita para:
E raiz quadrada de número negativo, não rola né? Então o sinal de vai depender somente do numerador. Assim, temos que, quando , o numerador é negativo e logo, toda a primeira derivada. E quando o numerador é positivo e, logo, a primeira derivada toda também será. Resumindo:
Os extremos relativos acontecem onde . Temos que apenas satisfaz isso, sendo o único extremo relativo.
Passo 5
- Definimos a concavidade de acordo com o sinal da derivada segunda: se for positiva, concavidade para cima; se negativa, para baixo. Vamos calcular a derivada segunda então!
Vamos fazer o quadro de sinais para analisar essa concavidade:
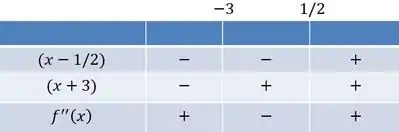
Nessa situação, a função tem concavidade para cima em e em e para baixo no resto do espaço. Como nosso domínio é , os intervalos passam a ser
- Para pensar em extremos absolutos temos que analisar se os limites da função para são maiores ou menores que os pontos críticos (onde ).
Já havíamos concluído que o limite de quando é . Como vemos que não haverão extremos absolutos, então!
- A imagem de consiste em todos os valores que ela pode assumir.
Como o limite de em é 3 e em e o limite explode para cima, considerando ainda concavidade sempre para cima, temos sua imagem:
Passo 6
- Agora juntamos todas as informações para desenhar o nosso gráfico.