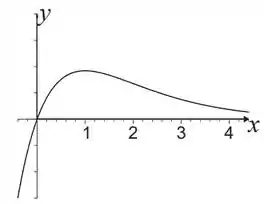
Esboce o gráfico de
Passo 1
Reescrevendo a função ela fica com essa cara:
Como , a função não possui restrições para o domínio. Logo,
Passo 2
Agora, vamos ver se a função tem alguma paridade, ou seja, se ela é uma função par ou uma função ímpar.
?
Não.
?
Não.
Passo 3
Agora temos que determinar se a função tem assíntotas. Vamos começar pelas verticais. Essas ocorrem perto de pontos de descontinuidade da função. Nesse caso, não temos.
Agora as assíntotas horizontais.
é assíntota horizontal.
Passo 4
Agora vamos ver crescimento da função, analisando o sinal da derivada.
Estudando o sinal da derivada temos o seguinte:
para DECRESCENTE
para CRESCENTE
Passo 5
Agora vamos determinar os máximos e mínimos da função, se existirem. Primeiro temos que achar os pontos críticos.
Como a derivada muda de positiva para negativa em , significa que esse é um máximo local da função. Nesse ponto a função vale
Podemos descobrir se ele é um máximo absoluto comparando o valor da função nesse ponto com os valores da função nas fronteiras do domínio. Como
significa que é máximo absoluto, pois
Passo 6
Falta estudar a concavidade da função.
Analisando o sinal:
e
Portanto:
- Quando a função tem concavidade para cima
- Quando a função tem concavidade para baixo
- O ponto é de inflexão.
Passo 7
Finalmente podemos esboçar o gráfico!
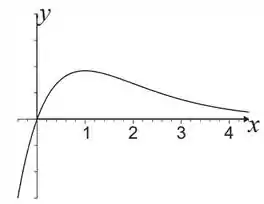
Passo 8
Passo 9
Resposta