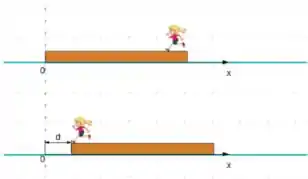
. Uma moça está parada no extremo direito de uma plataforma plana, que, por sua vez, também se encontra em repouso com relação à superfície de gelo em que se apoia. A moça, então, começa a correr para a esquerda com velocidade constante em relação à plataforma. Não há atrito entre a plataforma e a superfície de gelo, a massa da moça é , a massa da plataforma é e o tamanho da plataforma é . Tome a posição inicial do extremo esquerdo da plataforma em como mostrado na figura. Encontre o centro de massa do sistema (moça-plataforma) antes da moça começar a se mover. Quando a moça chega no extremo esquerdo da plataforma, esta se moveu uma distância (como na figura) determine .
Passo 1
Vem comigo que a gente da um jeito nessa questão!
Para encontrarmos o centro de massa antes da menina se mover, vamos usar a seguinte equação que nos fornece a posição do centro de massa:
Onde é a posição de um corpo do sistema até a origem.
Como só temos a menina e a barra no sistema a equação fica da seguinte maneira:
Mas a barra é um corpo extenso, como vamos fazer para achar a distância de cada pedaço dela até a origem?
Então, essa barra é homogênea, logo a distribuição de massa nela é igual, com isso o centro de massa dela sozinha é no meio dela, então podemos considerar o meio dela como a posição referente a origem.
Para achar a distância , temos que saber a velocidade da barra e o tempo que a menina levou para atravessar a barra inteira.
Para achar a velocidade, vamos usar a conservação de momento, já que a quantidade de movimento da menina é igual à da barra.
Tendo essa velocidade da barra, vamos subtrai-la da velocidade da menina em relação a barra para podermos encontrar a velocidade da menina em relação ao a superfície e encontrar o tempo que ela leva para percorrer .
Passo 2
Vamos encontrar primeiro o centro de massa, temos:
Substituindo com os valores que conhecemos, temos:
Assim temos que:
Passo 3
Agora vamos encontrar a velocidade da prancha, usando a conservação de momento, temos:
Substituindo os valores em módulo do que temos, ficamos com:
Assim temos que:
Passo 4
Agora vamos subtrair essa velocidade da velocidade da menina e encontrar a velocidade dela em relação a superfície. Temos:
Agora vamos usar uma equação, velha conhecida nossa, para achar o tempo que a menina leva para chegar na outra ponta da barra, temos:
Assim temos que:
Tendo esse tempo e sabendo a velocidade da barra, podemos achar o valor de , usando a mesma equação anterior, temos:
Com isso temos que:
Com isso finalizamos a questão!